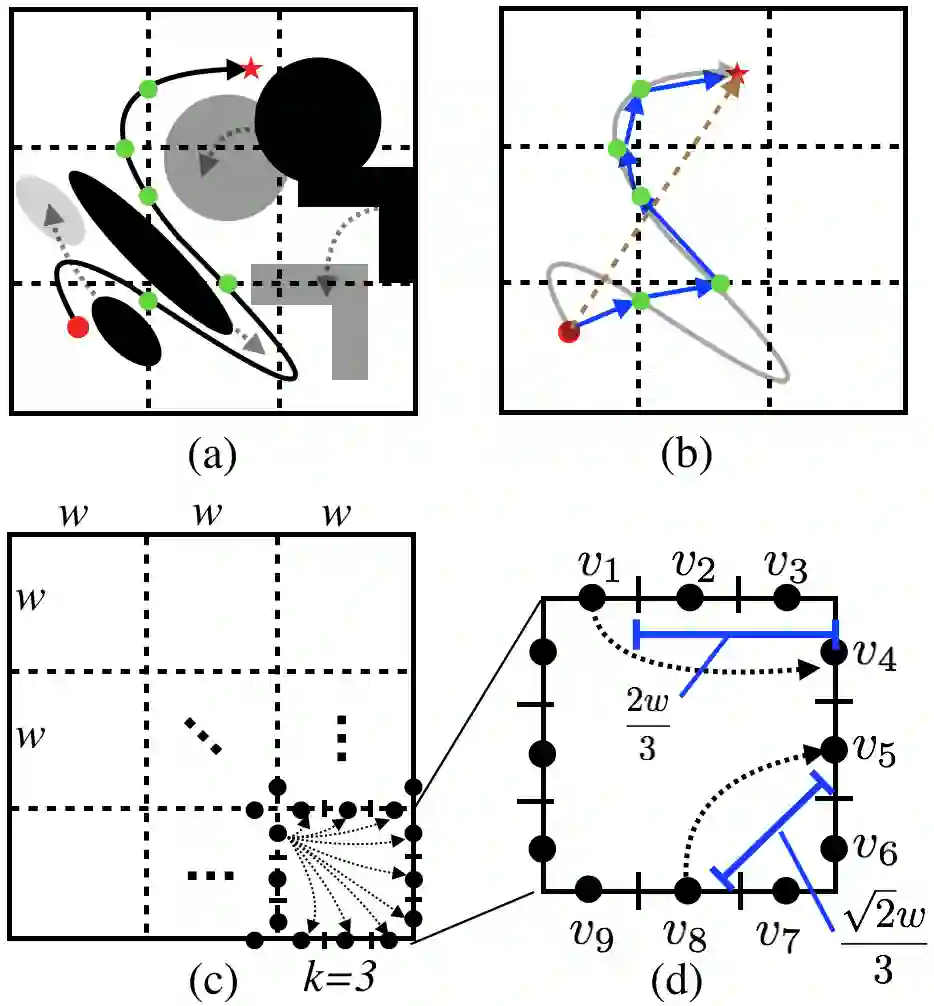
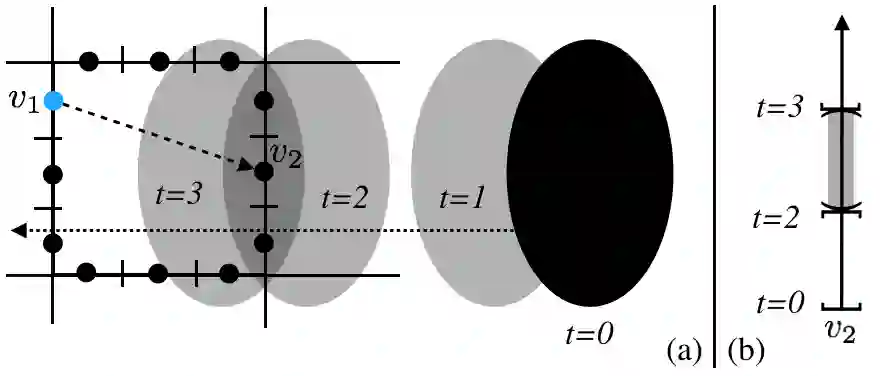
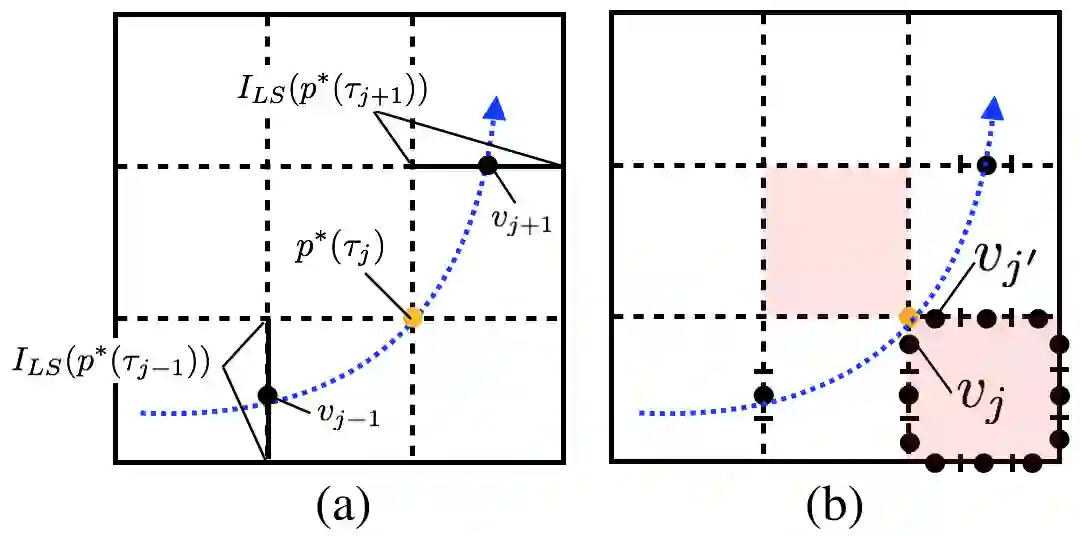
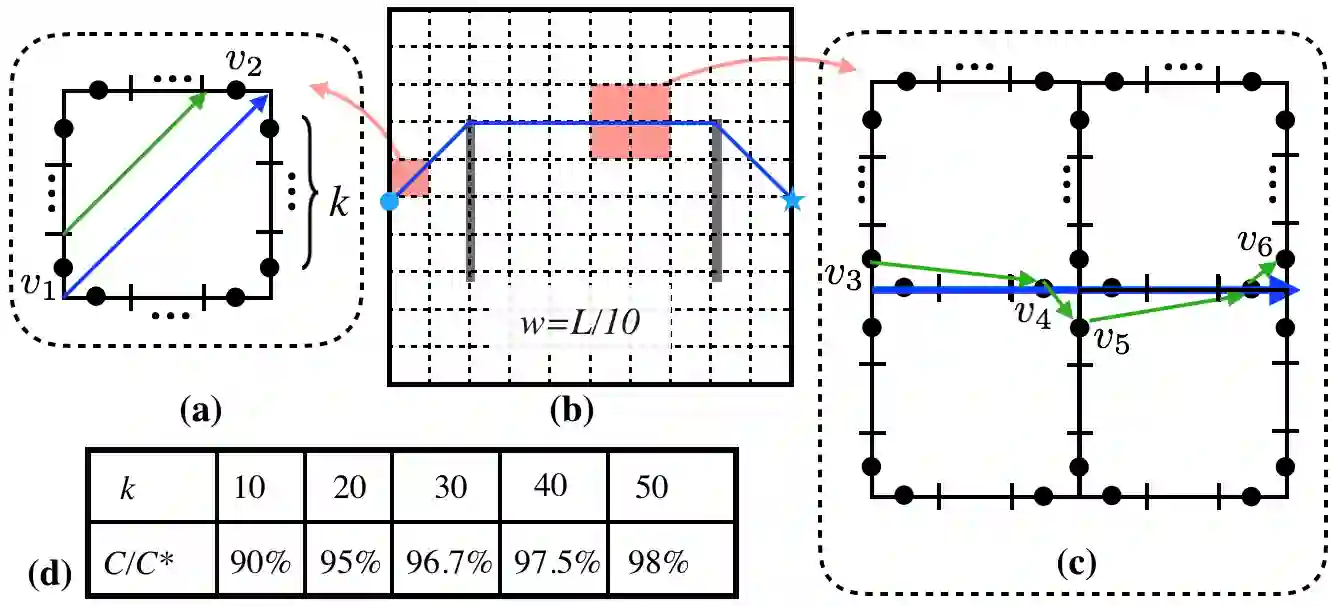
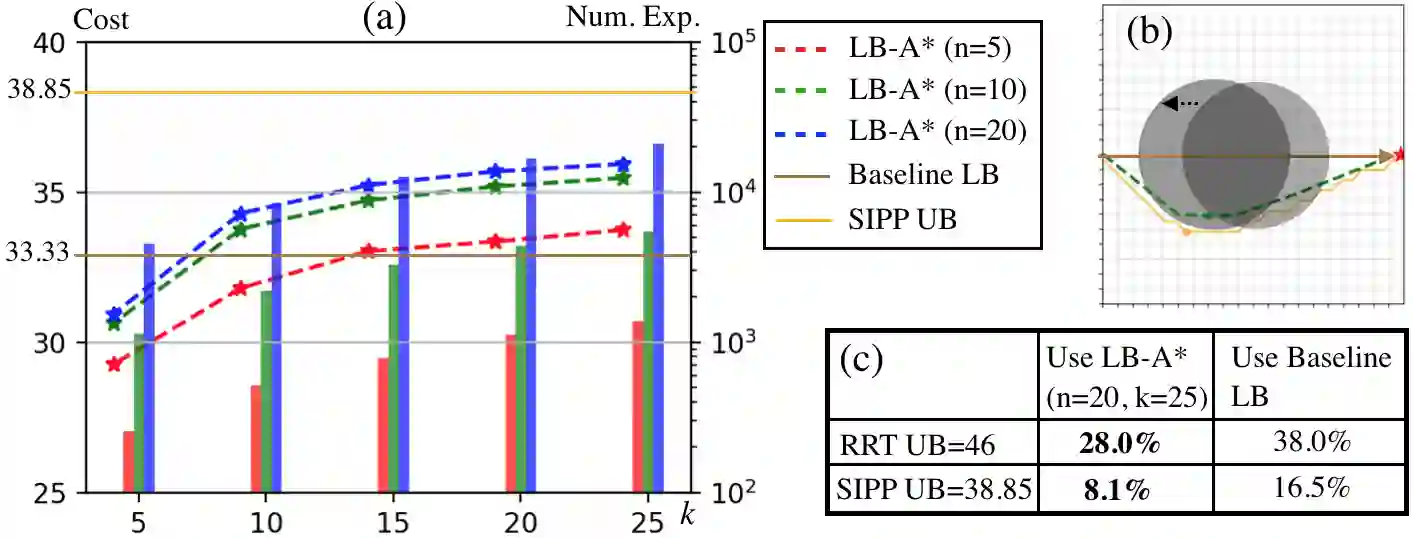
This work considers a Motion Planning Problem with Dynamic Obstacles (MPDO) in 2D that requires finding a minimum-arrival-time collision-free trajectory for a point robot between its start and goal locations amid dynamic obstacles moving along known trajectories. Existing methods, such as continuous Dijkstra paradigm, can find an optimal solution by restricting the shape of the obstacles or the motion of the robot, while this work makes no such assumptions. Other methods, such as search-based planners and sampling-based approaches can compute a feasible solution to this problem but do not provide approximation bounds. Since finding the optimum is challenging for MPDO, this paper develops a framework that can provide tight lower bounds to the optimum. These bounds act as proxies for the optimum which can then be used to bound the deviation of a feasible solution from the optimum. To accomplish this, we develop a framework that consists of (i) a bi-level discretization approach that converts the MPDO to a relaxed path planning problem, and (ii) an algorithm that can solve the relaxed problem to obtain lower bounds. We also present numerical results to corroborate the performance of the proposed framework. These results show that the bounds obtained by our approach for some instances are up to twice tighter than a baseline approach showcasing potential advantages of the proposed approach.
翻译:这项工作考虑了2D中具有动态障碍的动态规划问题(MPDO),它要求为其起始点和目标点位置之间的一个点机器人在已知轨道上移动的动态障碍中找到一个最低到达时间的无碰撞轨迹。现有的方法,例如连续的Dijkstra范式,可以通过限制障碍或机器人运动的形式找到最佳解决办法,而这项工作没有作出这样的假设。其他方法,例如搜索规划者和抽样方法,可以计算出解决这一问题的可行办法,但不能提供近似界限。由于找到最佳办法对MPDO来说具有挑战性,本文件开发了一个框架,可以使最佳范围更窄一些。这些界限作为最佳办法的代号,然后用来限制可行的解决办法与最佳办法的偏差。为了实现这一目标,我们制定了一个框架,包括(一) 将MPDO转换为宽松路径规划问题的双分化办法,以及(二) 一种能够解决宽松问题以获得较低界限的算法。我们还提出了一些数字结果,以证实我们提出的基准框架的更佳性办法,这些结果显示比更接近的更接近。
相关内容
Source: Apple - iOS 8