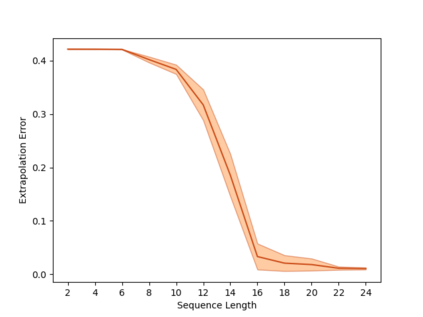
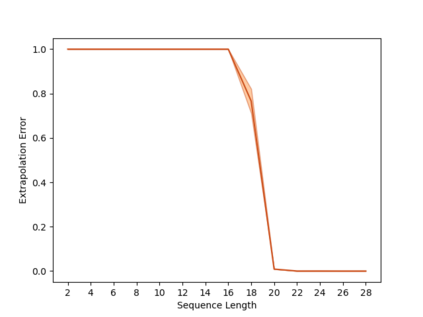
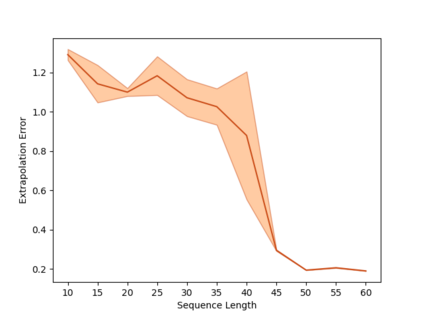
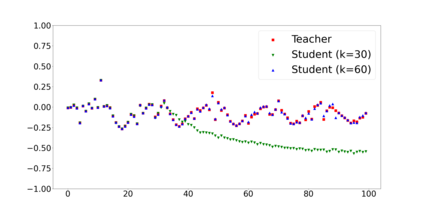
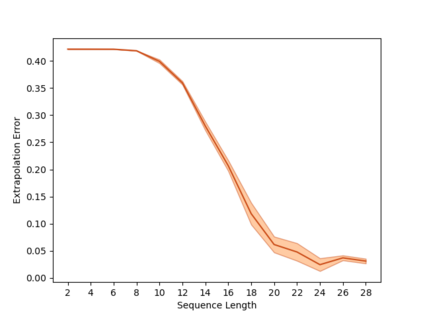
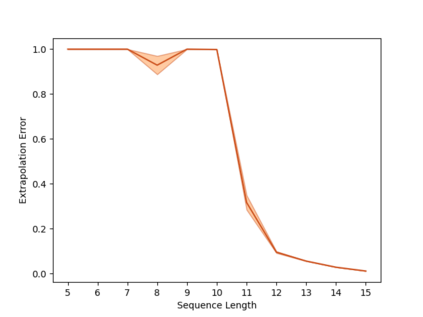
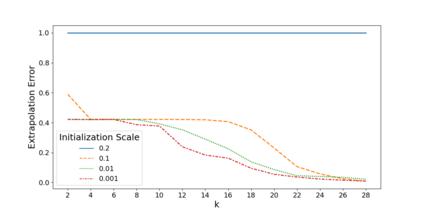
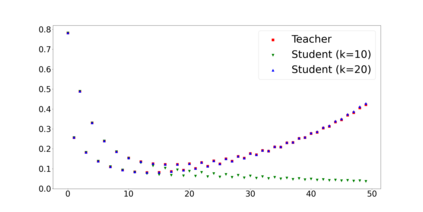
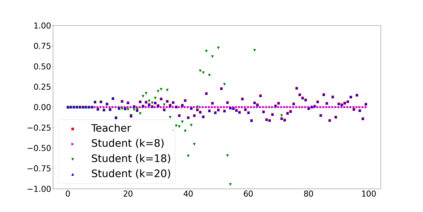
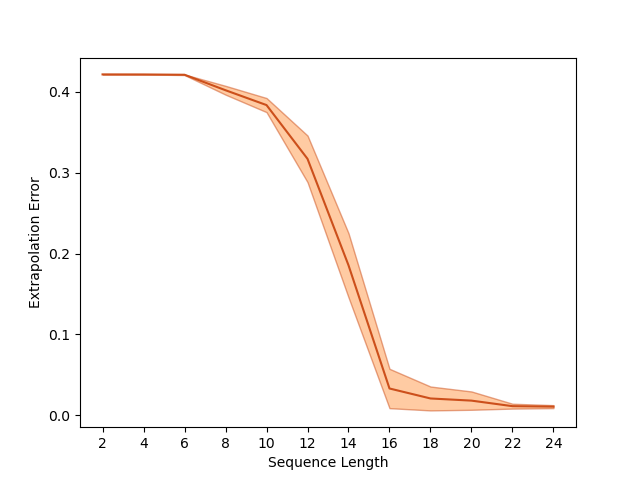
Overparameterization in deep learning typically refers to settings where a trained neural network (NN) has representational capacity to fit the training data in many ways, some of which generalize well, while others do not. In the case of Recurrent Neural Networks (RNNs), there exists an additional layer of overparameterization, in the sense that a model may exhibit many solutions that generalize well for sequence lengths seen in training, some of which extrapolate to longer sequences, while others do not. Numerous works have studied the tendency of Gradient Descent (GD) to fit overparameterized NNs with solutions that generalize well. On the other hand, its tendency to fit overparameterized RNNs with solutions that extrapolate has been discovered only recently and is far less understood. In this paper, we analyze the extrapolation properties of GD when applied to overparameterized linear RNNs. In contrast to recent arguments suggesting an implicit bias towards short-term memory, we provide theoretical evidence for learning low-dimensional state spaces, which can also model long-term memory. Our result relies on a dynamical characterization which shows that GD (with small step size and near-zero initialization) strives to maintain a certain form of balancedness, as well as on tools developed in the context of the moment problem from statistics (recovery of a probability distribution from its moments). Experiments corroborate our theory, demonstrating extrapolation via learning low-dimensional state spaces with both linear and non-linear RNNs.
翻译:在深度学习中,过参数化通常指训练的神经网络(NN)具有多种表示能力来拟合训练数据,其中一些具有推广性,而其他一些则没有。在递归神经网络(RNN)的情况下,存在一种额外的过参数化层面,其意义在于模型可能表现出许多在训练中看到的序列长度上具有很好推广能力的解决方案,其中一些可以外推到更长的序列,而其他一些则不能。许多研究探讨了梯度下降(GD)对于过参数化神经网络具有倾向性,使其具有可以很好推广的解决方案。另一方面,当应用于过参数化的RNN时,GD对其具有外推解决方案的倾向性最近才被发现,而且了解远不如前者。在这篇论文中,我们分析了当应用于过参数化的线性递归神经网络时,GD的外推性质。与最近提出的建议存在短期记忆的隐式偏差相反,我们提供了证据,证明GD可以学习低维状态空间,并能够建模长期记忆。我们的结果依赖于一种动态特征,该特征表明GD(使用小步长和接近零的初始化)努力保持一定的平衡形态,以及在统计学中(从其矩中恢复概率分布)的矩问题背景下开发的工具。实验证实了我们的理论,证明了使用线性和非线性RNN学习低维状态空间的外推能力。