【谷歌大脑新论文】利用可微摄动优化器进行学习，Learning with Differentiable Perturbed Optimizers

题目： Learning with Differentiable Perturbed Optimizers

摘 要:

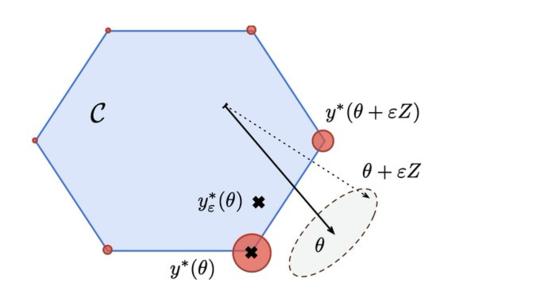
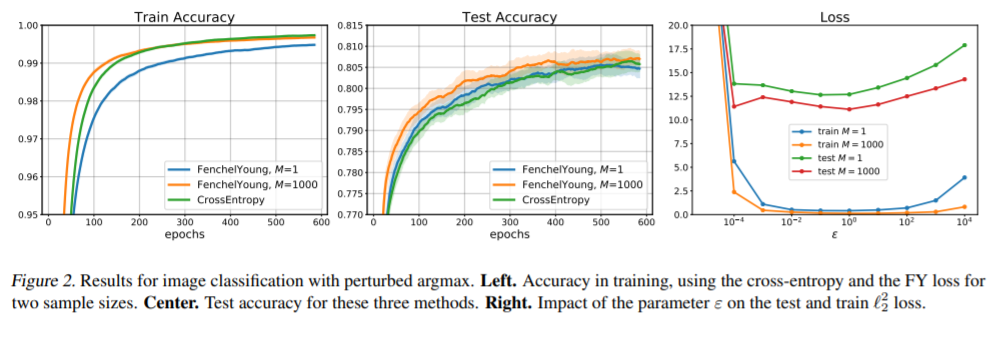
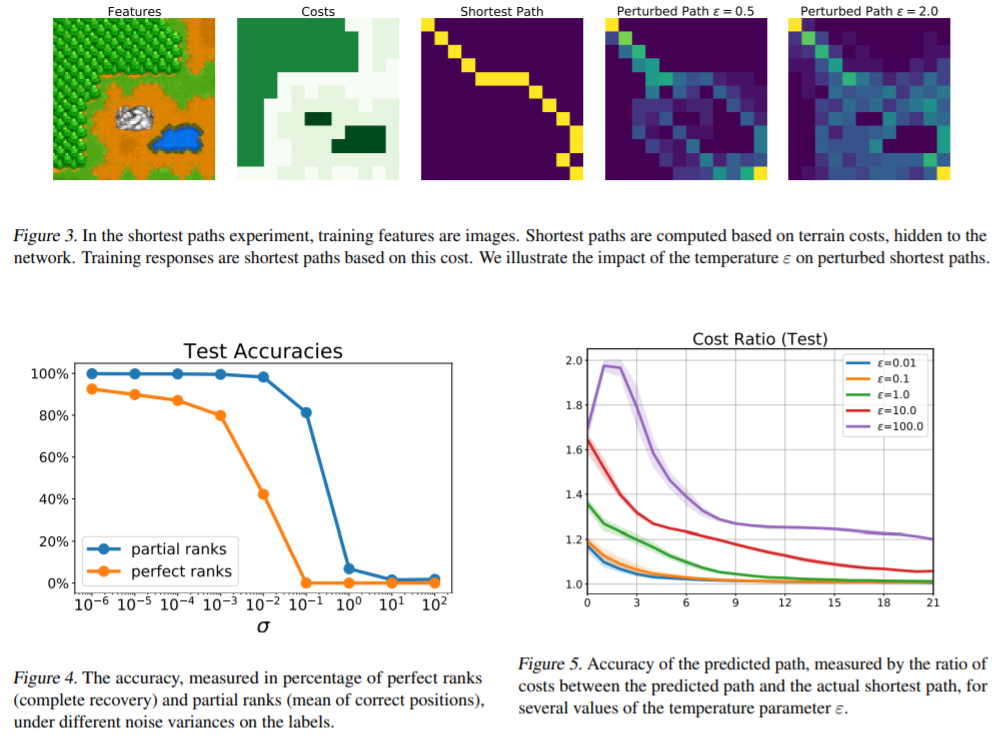
机器学习管道通常依赖于优化过程来做出离散的决策(例如排序、挑选最近的邻居、寻找最短路径或最佳匹配)。虽然这些离散的决策很容易以正向的方式进行计算，但它们不能用于使用一阶优化技术修改模型参数，因为它们破坏了计算图的反向传播。为了扩展端到端的学习问题的范围，提出了一种将输出最优离散决策的块转换为可微操作的系统方法。我们的方法依赖于这些参数的随机扰动，并且可以很容易地在现有的求解器中使用，而不需要特别的正则化或平滑。这些扰动的优化器得到的解是可微的，且不满足局部常数。平滑度的大小可以通过选择的噪声幅值进行调整，我们分析了噪声幅值的影响。这些扰动解的导数可以得到有效的评价。我们还展示了该框架如何与结构化预测中产生的一系列损失相联系，并描述了如何在有理论保证的情况下，在无监督和监督学习中使用这些损失。我们在模拟和真实数据的实验中证明了我们的方法在几个机器学习任务中的性能。