Invertible ResNets for Inverse Imaging Problems: Competitive Performance with Provable Regularization Properties

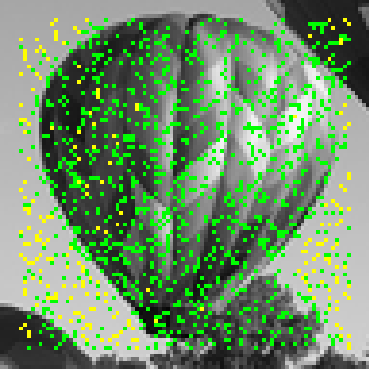
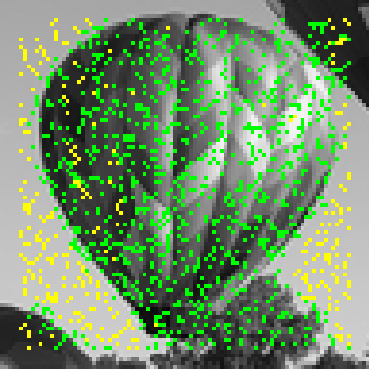
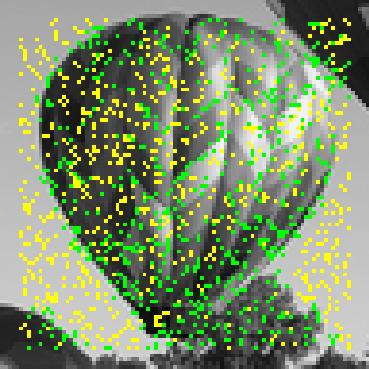
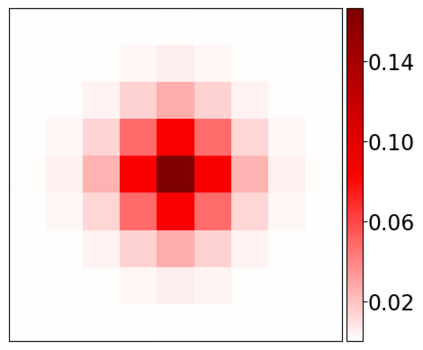
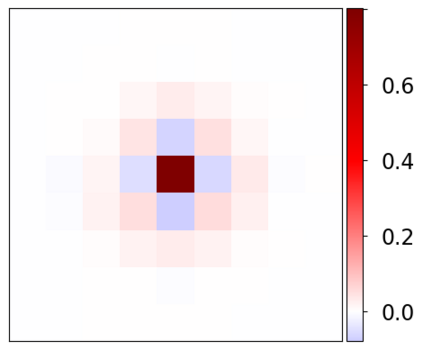
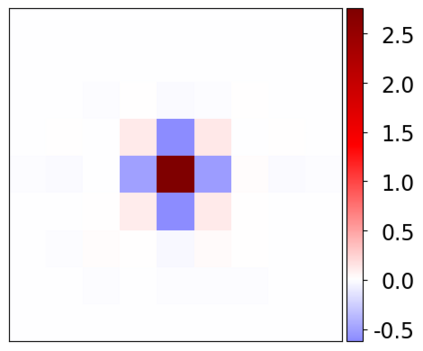
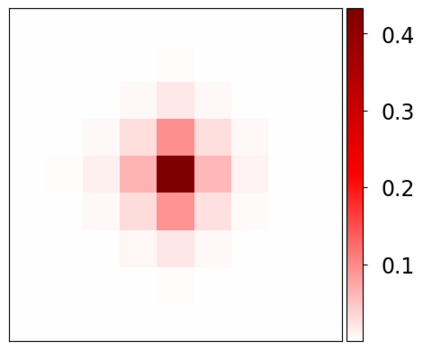
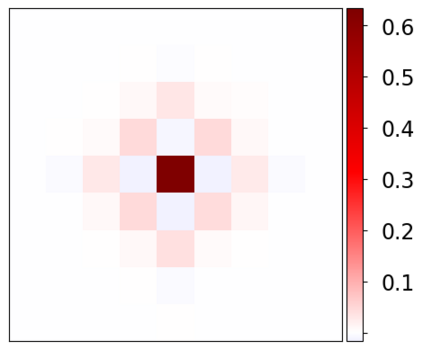
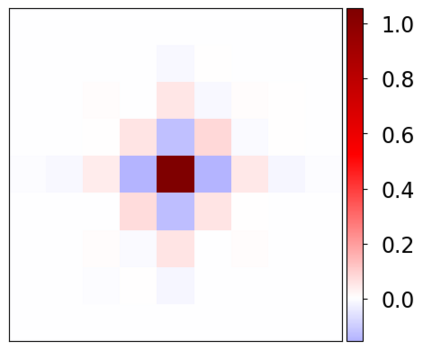
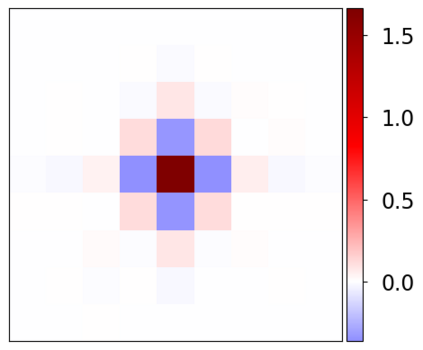
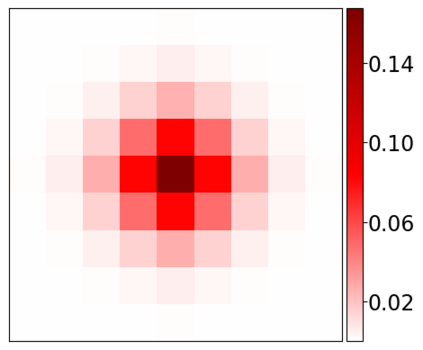
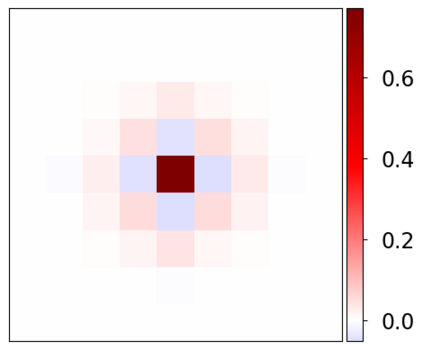
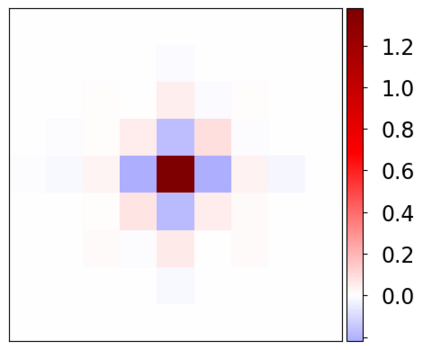
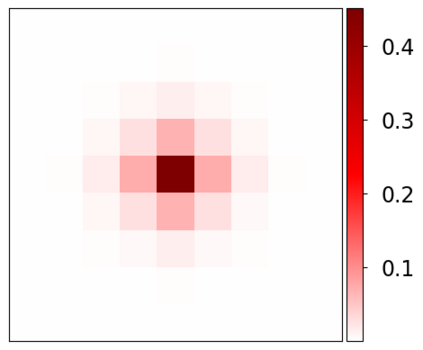
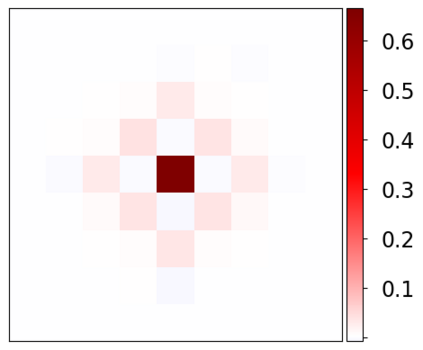
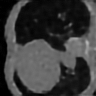
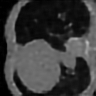
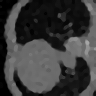
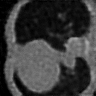
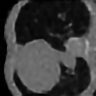
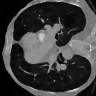
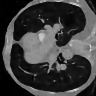
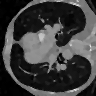
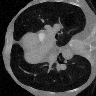
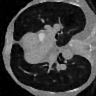
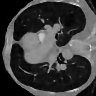
Learning-based methods have demonstrated remarkable performance in solving inverse problems, particularly in image reconstruction tasks. Despite their success, these approaches often lack theoretical guarantees, which are crucial in sensitive applications such as medical imaging. Recent works by Arndt et al addressed this gap by analyzing a data-driven reconstruction method based on invertible residual networks (iResNets). They revealed that, under reasonable assumptions, this approach constitutes a convergent regularization scheme. However, the performance of the reconstruction method was only validated on academic toy problems and small-scale iResNet architectures. In this work, we address this gap by evaluating the performance of iResNets on two real-world imaging tasks: a linear blurring operator and a nonlinear diffusion operator. To do so, we compare the performance of iResNets against state-of-the-art neural networks, revealing their competitiveness at the expense of longer training times. Moreover, we numerically demonstrate the advantages of the iResNet's inherent stability and invertibility by showcasing increased robustness across various scenarios as well as interpretability of the learned operator, thereby reducing the black-box nature of the reconstruction scheme.