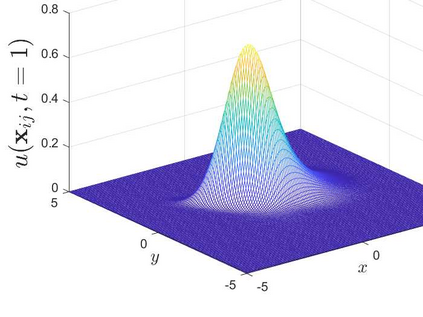
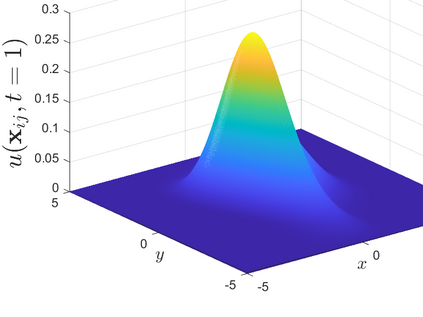
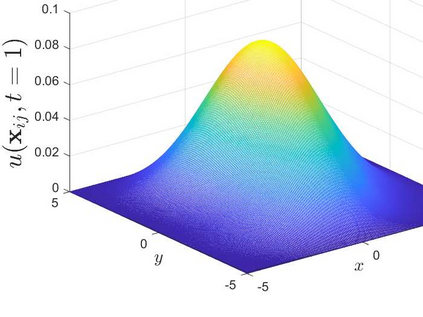
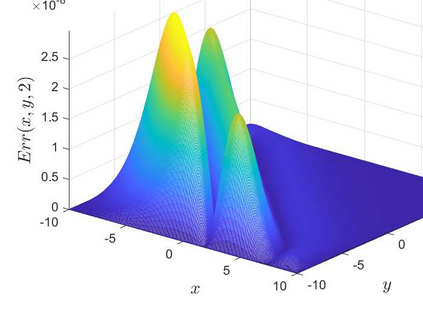
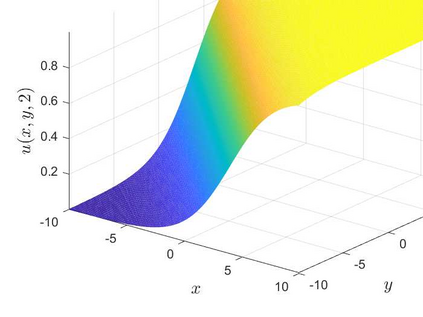
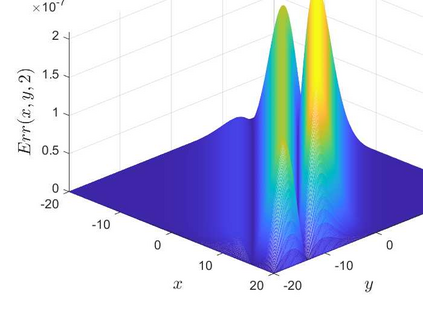
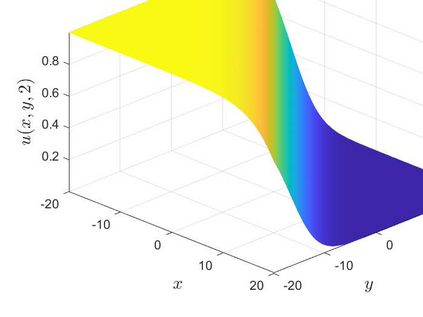
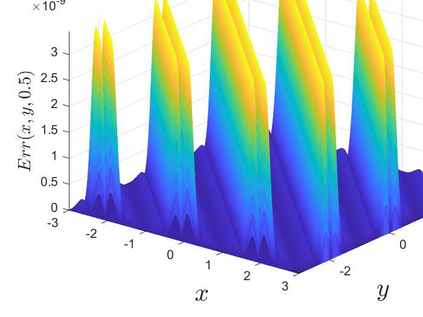
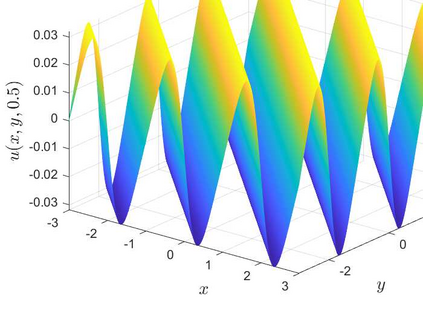
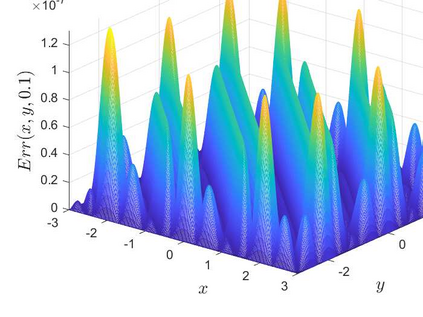
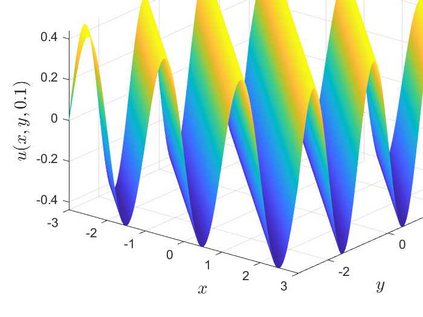
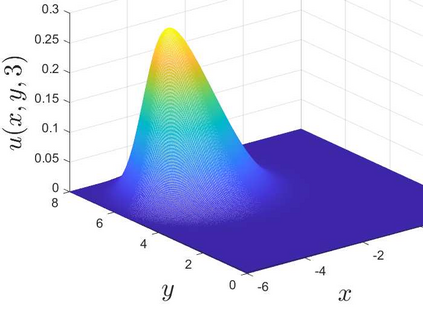
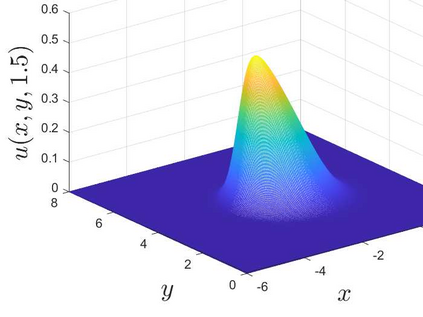
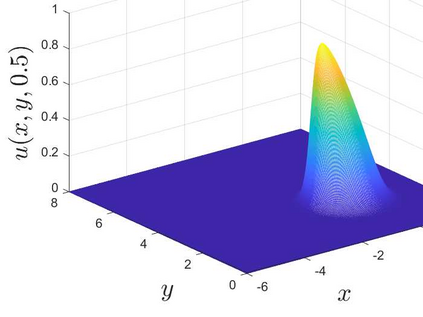
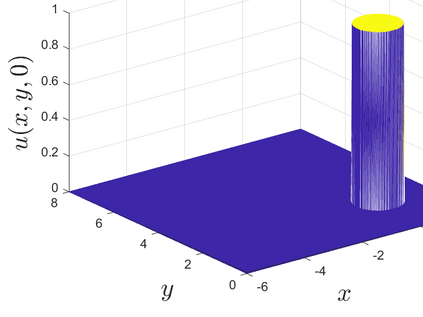
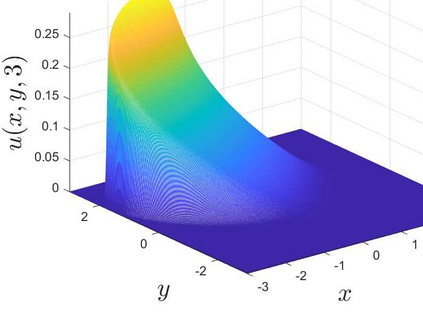
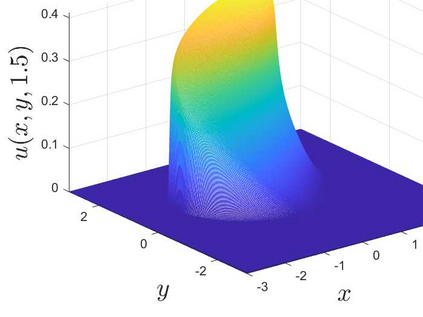
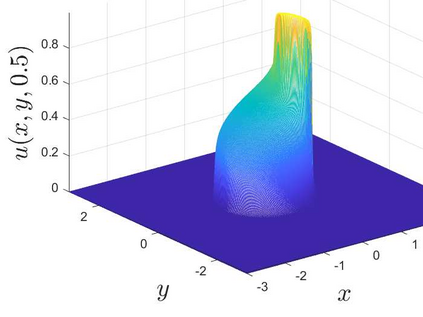
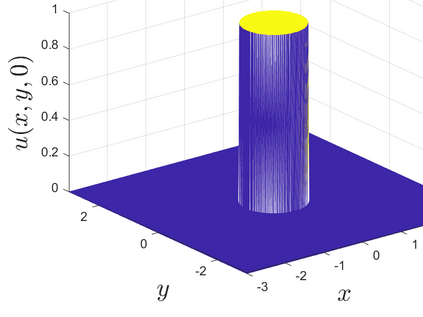
This is the second part of study on the optimal convergence rate of the explicit Euler discretization in time for the convection-diffusion equations [Appl. Math. Lett. \textbf{131} (2022) 108048] which focuses on high-dimensional linear/nonlinear cases under Dirichlet or Neumann boundary conditions. Several new corrected difference schemes are proposed based on the explicit Euler discretization in temporal derivative and central difference discretization in spatial derivatives. The priori estimate of the corrected scheme with application to constant convection coefficients is provided at length by the maximum principle and the optimal convergence rate four is proved when the step ratios along each direction equal to $1/6$. The corrected difference schemes have essentially improved {\rm \textbf{CFL}} condition and the numerical accuracy comparing with the classical difference schemes. Numerical examples involving two-/three-dimensional linear/nonlinear problems under Dirichlet/Neumann boundary conditions such as the Fisher equation, the Chafee-Infante equation, the Burgers' equation and classification to name a few substantiate the good properties claimed for the corrected difference scheme.
翻译:这是关于对流-扩散方程式[Appl. Math. Lett.\ textbf{131} (2022) 108048] 明确分解率的最佳趋同率研究的第二部分,重点是Drichlet或Neumann边界条件下的高维线性/非线性案例。根据时间衍生物的明显分解和空间衍生物的中央分解,提出了几项新的纠正差异方案。经更正的适用于常态对流系数的方案的先验估计,由最高原则提供时间长度,而最佳合并率四在每一方向的阶梯比率等于1/6美元时得到证明。经更正的差别方案基本上改进了\rm\ textbf{CFL}}条件和与传统差异方案相比的数字准确性。Drichlet/Neumann边界条件下的两维线性/三维线性/非线性问题,如Fisherality、Chafee-Infante等方程式、Burgers的方程式和分类,以少数证据证明为经更正的差异。