A hidden Markov modeling approach combining objective measure of activity and subjective measure of self-reported sleep to estimate the sleep-wake cycle

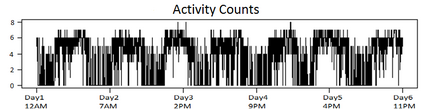
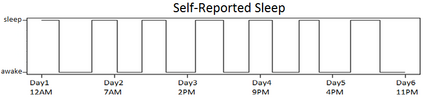
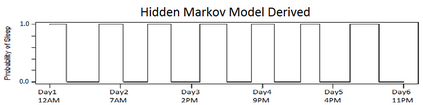
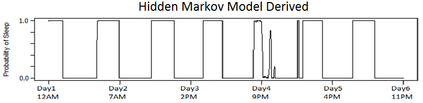
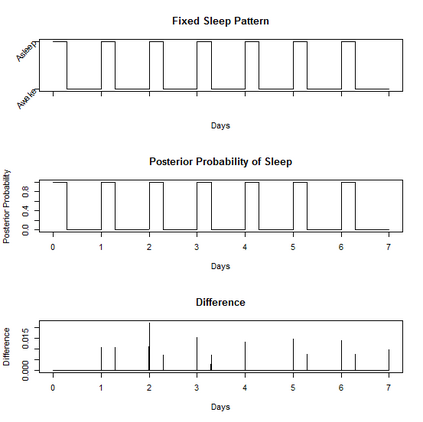
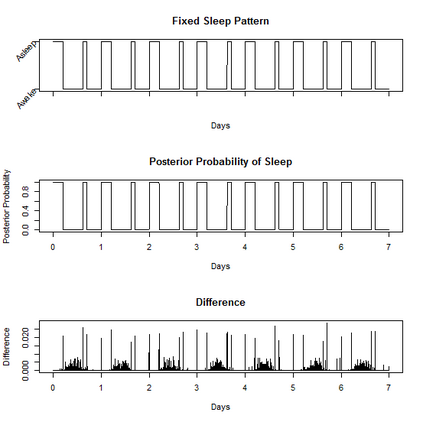
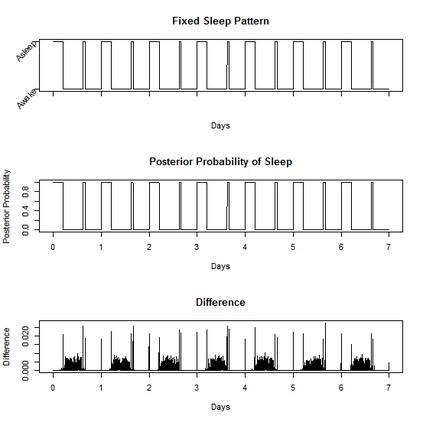
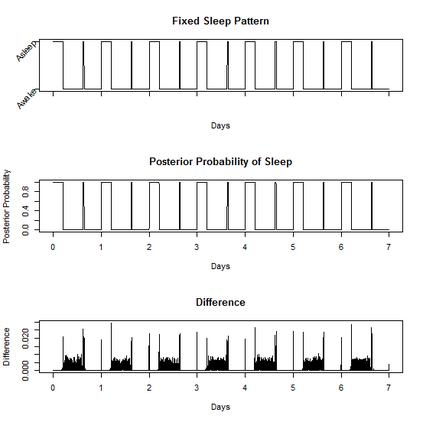
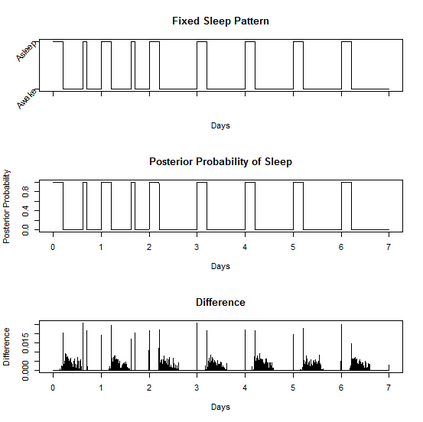
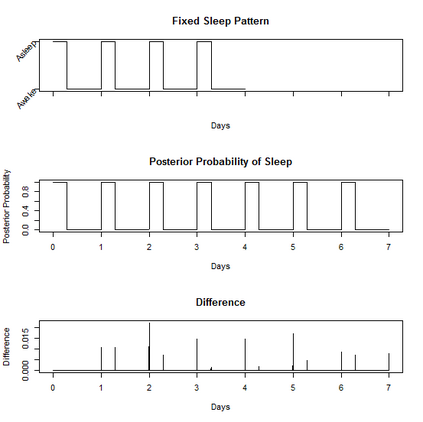
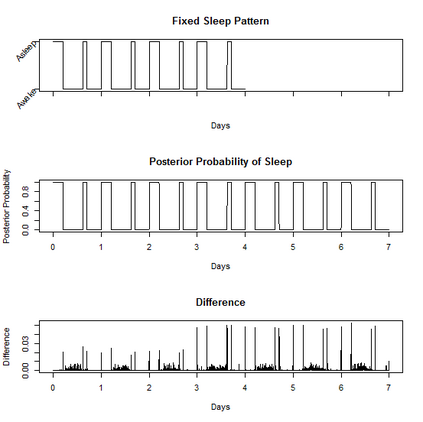
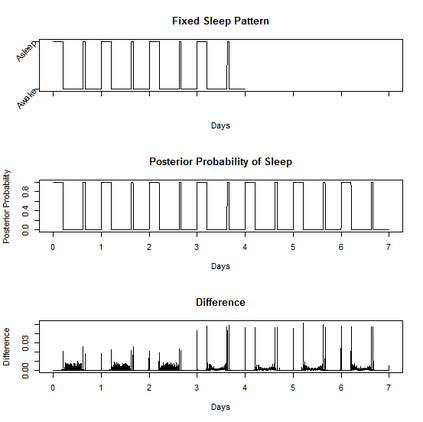
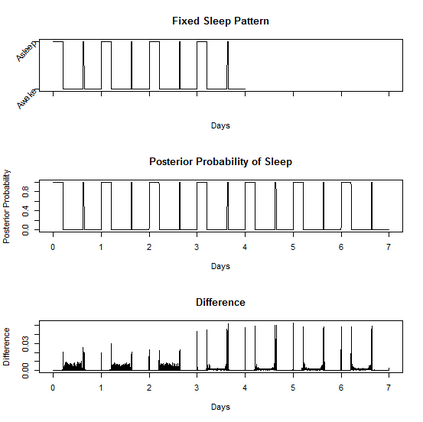
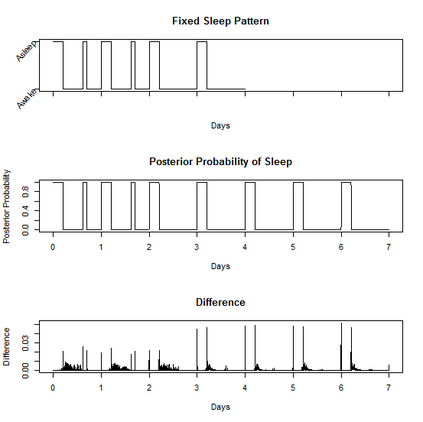
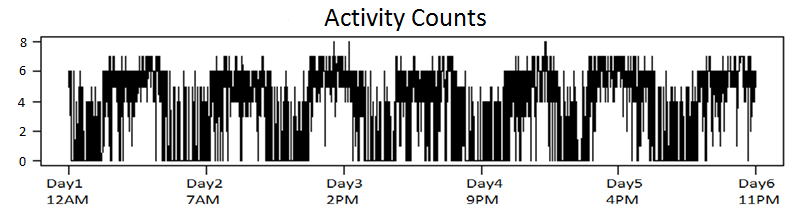
Characterizing the sleep-wake cycle in adolescents is an important prerequisite to better understand the association of abnormal sleep patterns with subsequent clinical and behavioral outcomes. The aim of this research was to develop hidden Markov models (HMM) that incorporate both objective (actigraphy) and subjective (sleep log) measures to estimate the sleep-wake cycle using data from the NEXT longitudinal study, a large population-based cohort study. The model was estimated with a negative binomial distribution for the activity counts (1-minute epochs) to account for overdispersion relative to a Poisson process. Furthermore, self-reported measures were dichotomized (for each one-minute interval) and subject to misclassification. We assumed that the unobserved sleep-wake cycle follows a two-state Markov chain with transitional probabilities varying according to a circadian rhythm. Maximum-likelihood estimation using a backward-forward algorithm was applied to fit the longitudinal data on a subject by subject basis. The algorithm was used to reconstruct the sleep-wake cycle from sequences of self-reported sleep and activity data. Furthermore, we conduct simulations to examine the properties of this approach under different observational patterns including both complete and partially observed measurements on each individual.