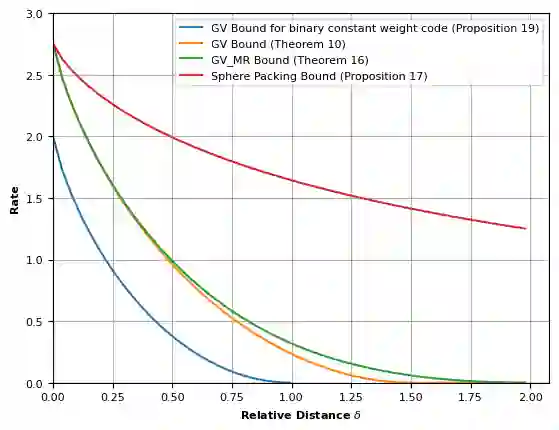
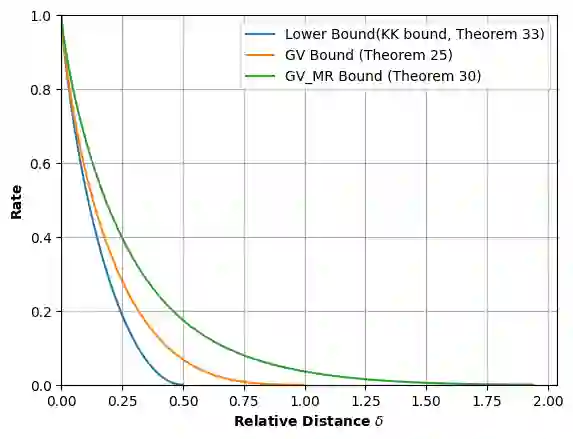
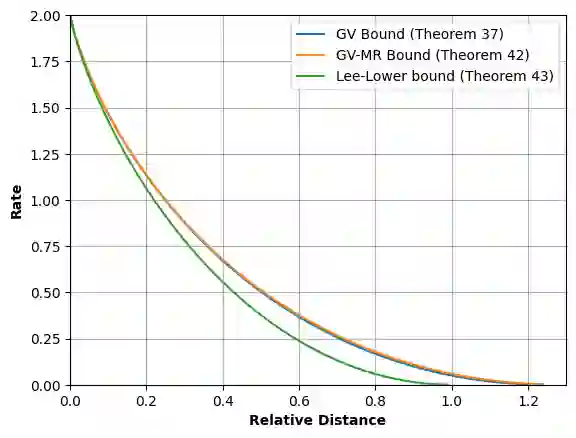
Analytic combinatorics in several variables refers to a suite of tools that provide sharp asymptotic estimates for certain combinatorial quantities. In this paper, we apply these tools to determine the Gilbert--Varshamov lower bound on the rate of optimal codes in $L_1$ metric. Several different code spaces are analyzed, including the simplex and the hypercube in $\mathbb{Z^n}$, all of which are inspired by concrete data storage and transmission models such as the sticky insertion channel, the permutation channel, the adjacent transposition (bit-shift) channel, the multilevel flash memory channel, etc.
翻译:暂无翻译
相关内容
专知会员服务
34+阅读 · 2019年10月18日
专知会员服务
36+阅读 · 2019年10月17日
Arxiv
17+阅读 · 2022年5月10日
Arxiv
27+阅读 · 2021年1月21日
InteractE: Improving Convolution-based Knowledge Graph Embeddings by Increasing Feature Interactions
Arxiv
13+阅读 · 2019年11月1日
Arxiv
17+阅读 · 2018年3月20日