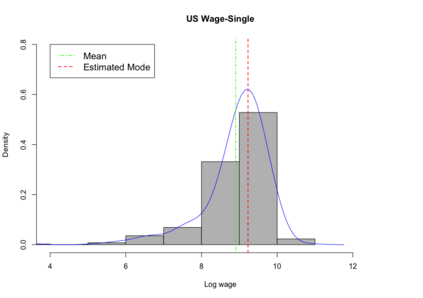
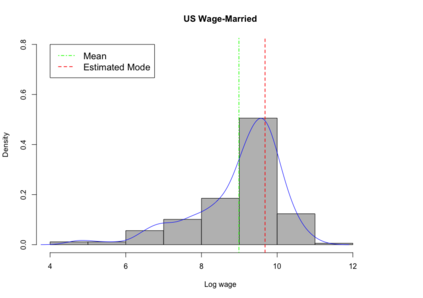
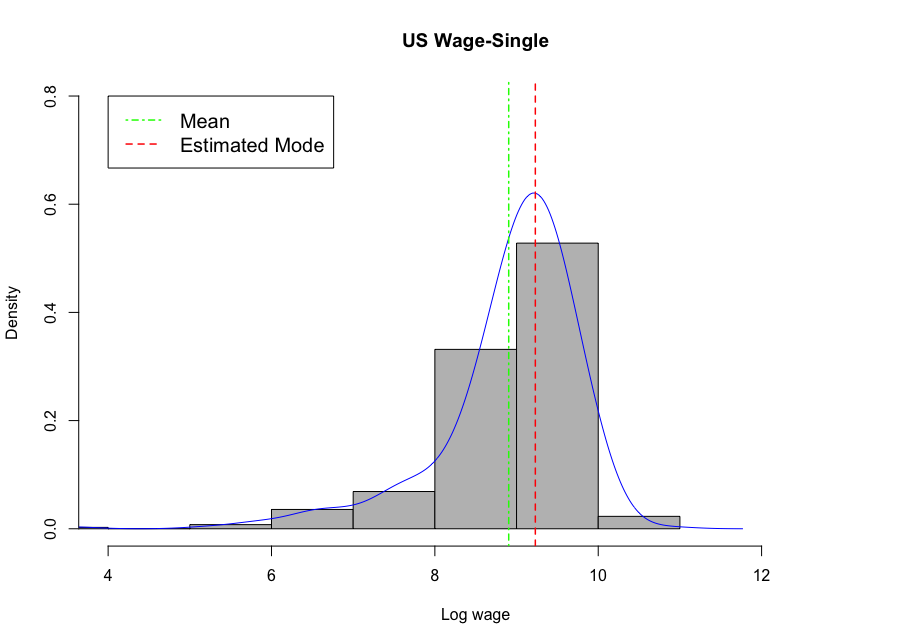
In this paper, we develop uniform inference methods for the conditional mode based on quantile regression. Specifically, we propose to estimate the conditional mode by minimizing the derivative of the estimated conditional quantile function defined by smoothing the linear quantile regression estimator, and develop two bootstrap methods, a novel pivotal bootstrap and the nonparametric bootstrap, for our conditional mode estimator. Building on high-dimensional Gaussian approximation techniques, we establish the validity of simultaneous confidence rectangles constructed from the two bootstrap methods for the conditional mode. We also extend the preceding analysis to the case where the dimension of the covariate vector is increasing with the sample size. Finally, we conduct simulation experiments and a real data analysis using U.S. wage data to demonstrate the finite sample performance of our inference method.
翻译:在本文中,我们开发了基于四分位回归的有条件模式的统一推断方法。 具体地说, 我们提议通过最大限度地减少通过平滑线性四分位回归测算仪定义的估算的有条件量化函数的衍生物来估计有条件模式, 并为我们的有条件模式测算仪开发两种陷阱方法, 一个新的枢轴测算器和非参数测算器。 我们以高斯高斯近距离近比技术为基础, 确定从两种测算器方法中为有条件模式构建的同步信任矩形的有效性。 我们还将前述分析扩展至当共变矢量的尺寸随着样本大小而增加时的情况。 最后, 我们用美国的工资数据进行模拟实验和真实的数据分析, 以展示我们推断方法的有限样本性能 。