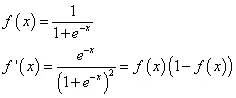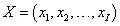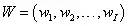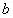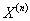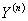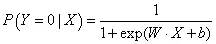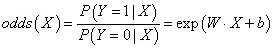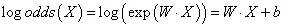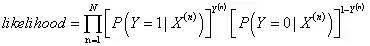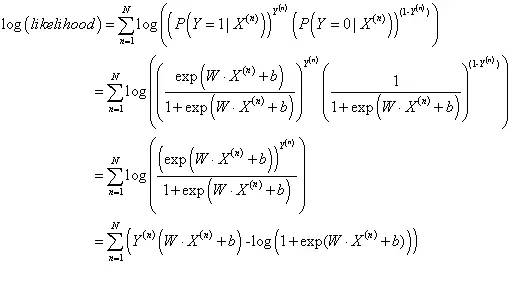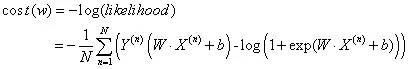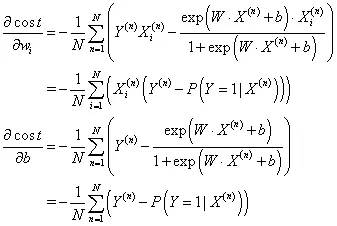Logistic回归第一弹——二项Logistic Regression

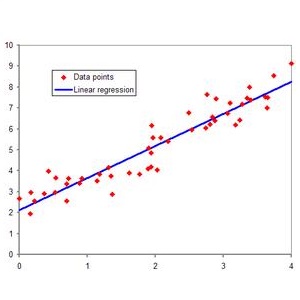
当目标变量是连续值时，通常可以用线性回归模型来确定两种或两种以上变量间相互依赖的定量关系，然而当目标变量是离散值的时候，回归分析的方法还好用吗？答案是肯定的，而是威力十足。首先我们先来回顾一下线性回归的模型：
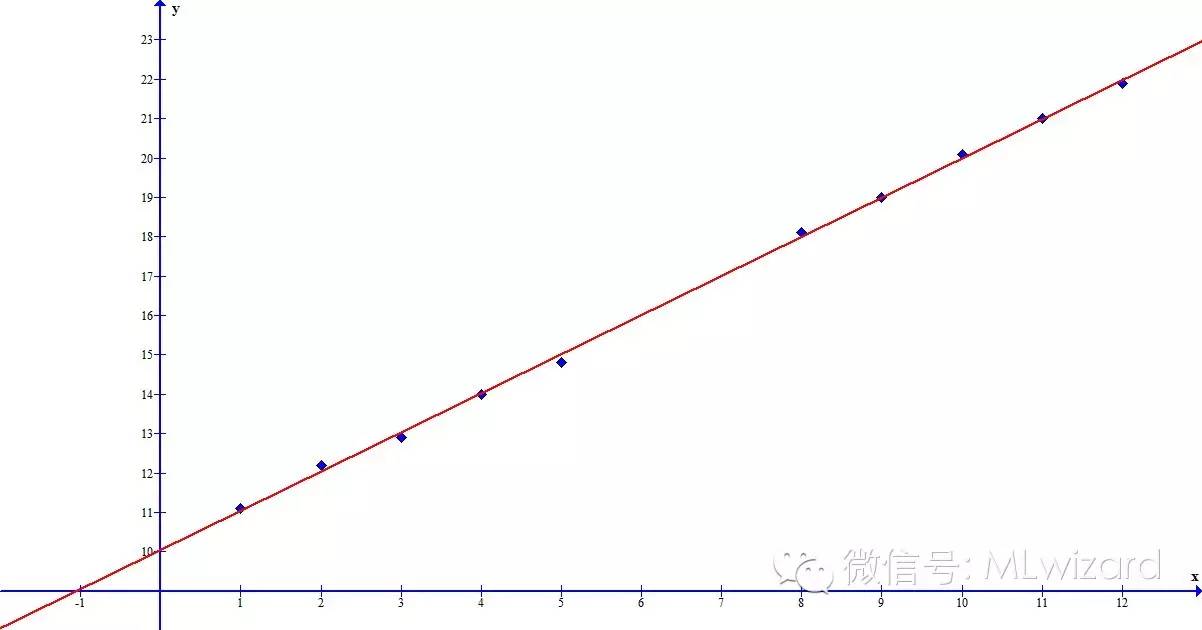
，当目标变量为连续值时，通常可以用线性模型来描述二者之间的关系：

图1

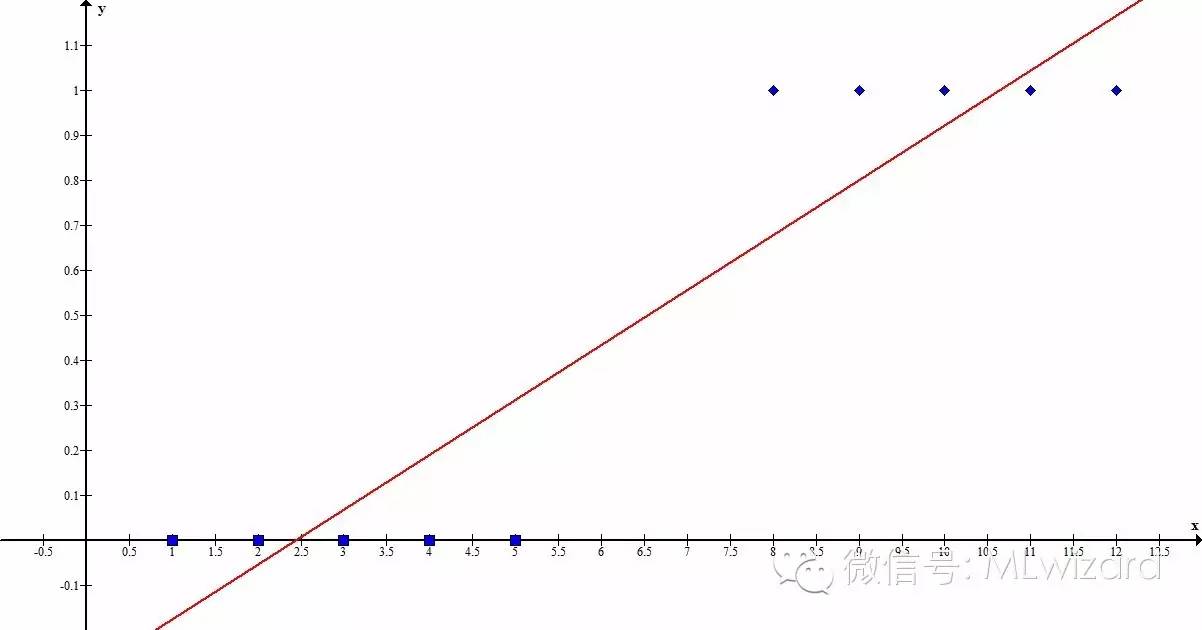
然而当目标变量为离散值时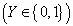，线性模型的拟合效果就会变得很差。

图2

这个种情形下，直接应用线性模型的确有些勉为其难，Logistic回归模型将完美的解决这一问题。正式开讲Logistic回归模型之前，先隆重介绍一下神奇的logistic函数：

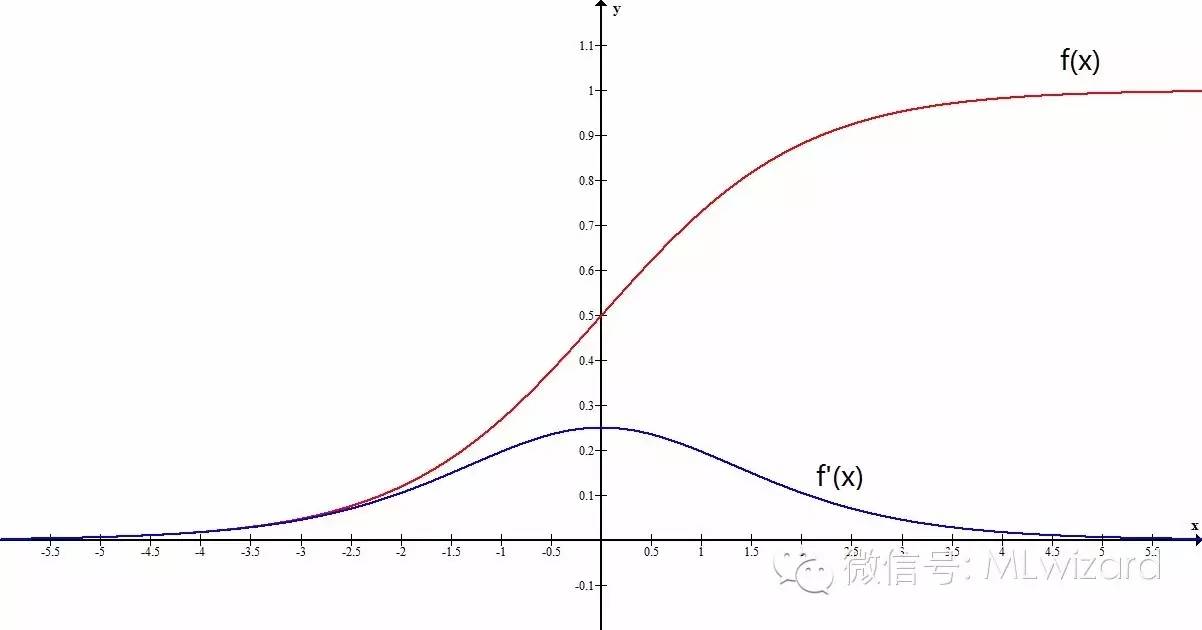
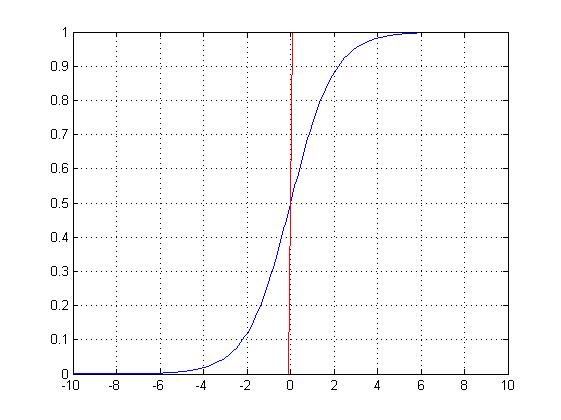
Logisitc函数及其一阶导数

图3

图3为logistic函数及其一阶导数的图像，将其与图2中的散点对比一下，有没有觉得有一种亲切感？只要将logistic函数稍作拉伸和偏移，二者便可擦出下面的火花：

图4

有了神奇的logistic函数，logistic回归模型呼之欲出。

模型定义

输入向量维度：I

输入向量：
权值向量：
截距项：
训练样本编号：
第n个样本输入变量：
第n个样本目标变量：
目标变量分类个数：2

定义事件A，当Y=1时A发生，Y=0时A不发生。在给定输入变量X的情况下，

A发生的条件概率：

A不发生的条件概率：

事件的几率

一个事件的几率（odds）指的该事件发生的概率与不发生的概率的比值。在给定输入变量X的情况下，

A的几率：

A的对数几率：

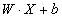
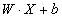
进过对数运算后，不难发现事件A（即Y=1）的对数几率是输入X的线性函数，这便是——Logistic回归模型。换一个角度来看，考虑对输入X进行分类的线性函数，其值域为实数域。通过模型定义式（1.1）可以将线性函数转换为概率：

此时，线性函数的值越接近正无穷，概率值越接近与1；线性函数的值越接近负无穷，概率值越接近于0。

参数估计

对于给定的训练数据集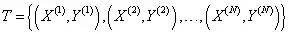，可以应用极大似然估计的方法对模型做参数估计。

模型似然值

模型对数似然值

损失函数

可以证明，该损失函数为凸函数，存在极小值。令损失函数取小值的W即为模型的极大似然估计。最易实现的方法是应用梯度下降进行参数训练。

损失函数的一阶偏导数

算法核心程序

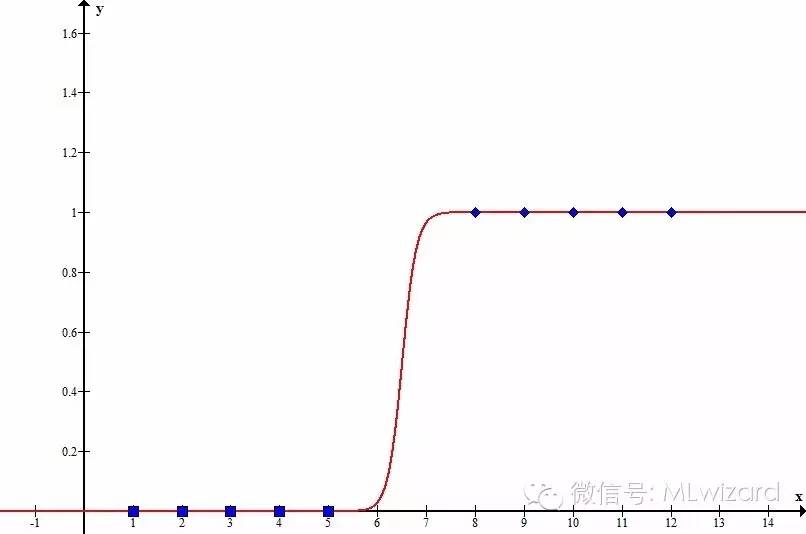
小试牛刀

采用经典的分类数据——鸢尾花卉数据集（http://archive.ics.uci.edu/ml/datasets/Iris）进行测试。由于本文介绍的二项logisitc回归模型目前只能处理二元分类问题，而源文件中目标分类个数为3，超出了本文的能力范围，因此选取前2个类别的数据进行建模。采用随机抽样的方法，将鸢尾花卉数据集的前100行分割成训练和测试两个数据集，其中训练数据64条，测试数据36条。测试结果如下：

测试数据下载地址：http://pan.baidu.com/s/1hqm7cuo。

小结

本文简单介绍了二项Logistic Regression模型的基本理论与算法实现。通过测试数据可以看到，二项Logistic Regression分类器处理二元分类问题时的确威力十足，然而当遇到多分类问题时应该怎么办呢？敬请期待Logistic回归第二弹——Softmax Regression。