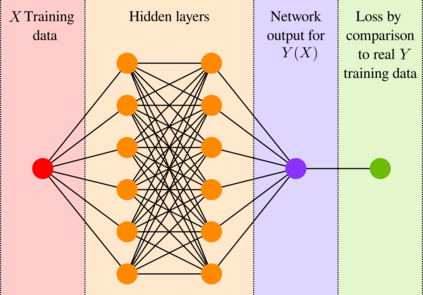
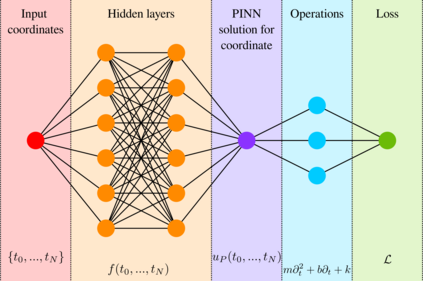
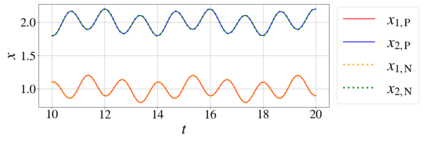
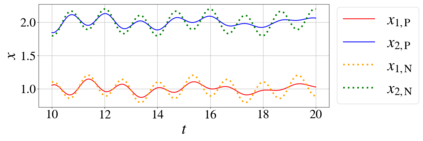
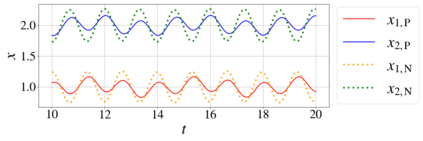
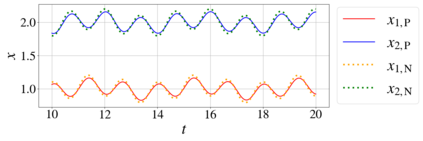
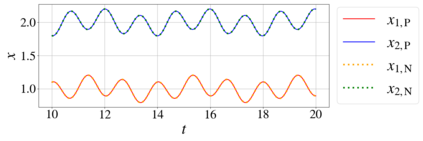
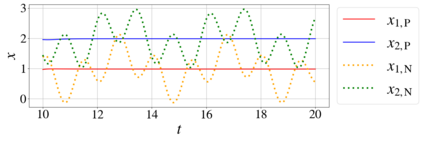
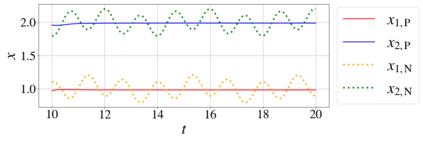
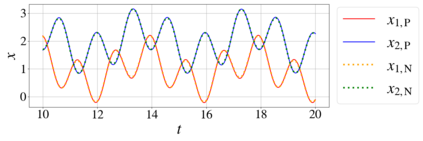
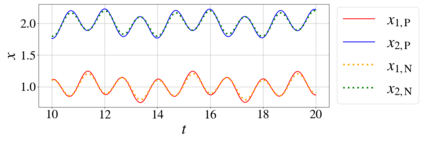
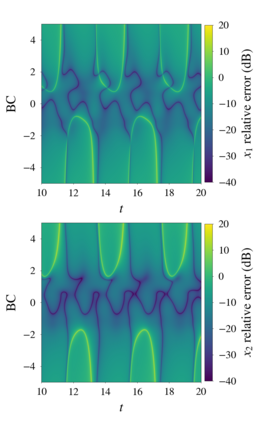
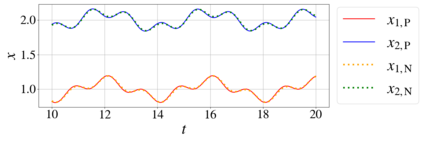
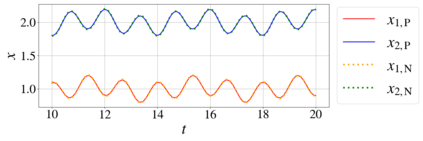
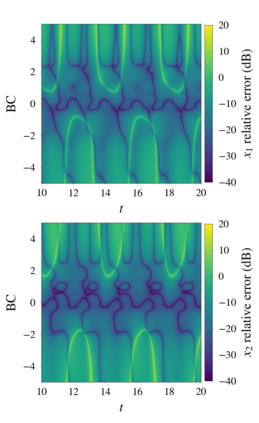
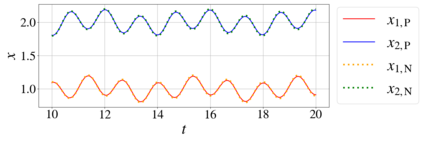
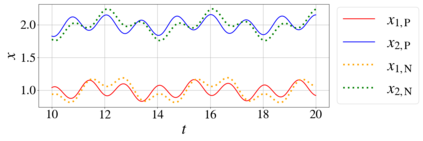
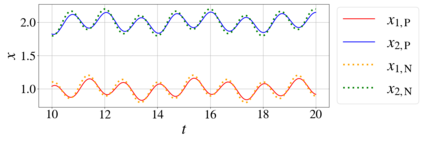
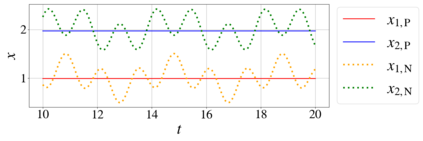
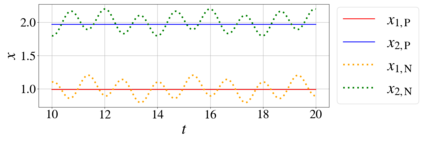
In this paper, we introduce a formulation of Physics-Informed Neural Networks (PINNs), based on learning the form of the Fourier decomposition, and a training methodology based on a spread of randomly chosen boundary conditions. By training in this way we produce a PINN that generalises; after training it can be used to correctly predict the solution for an arbitrary set of boundary conditions and interpolate this solution between the samples that spanned the training domain. We demonstrate for a toy system of two coupled oscillators that this gives the PINN formulation genuine predictive capability owing to an effective reduction of the training to evaluation times ratio due to this decoupling of the solution from specific boundary conditions.
翻译:暂无翻译