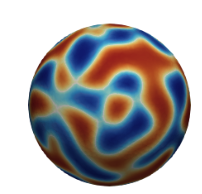
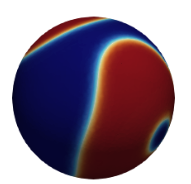
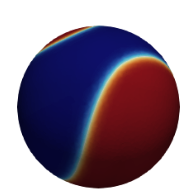
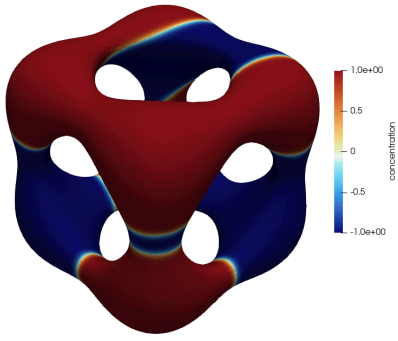
This paper addresses the analysis and numerical assessment of a computational method for solving the Cahn--Hilliard equation defined on a surface. The proposed approach combines the stabilized trace finite element method for spatial discretization with an implicit--explicit scheme for temporal discretization. The method belongs to a class of unfitted finite element methods that use a fixed background mesh and a level-set function for implicit surface representation. We establish the numerical stability of the discrete problem by showing a suitable energy dissipation law for it. We further derive optimal-order error estimates assuming simplicial background meshes and finite element spaces of order $m \geq 1$. The effectiveness of the method is demonstrated through numerical experiments on several two-dimensional closed surfaces, confirming the theoretical results and illustrating the robustness and convergence properties of the scheme.
翻译:暂无翻译