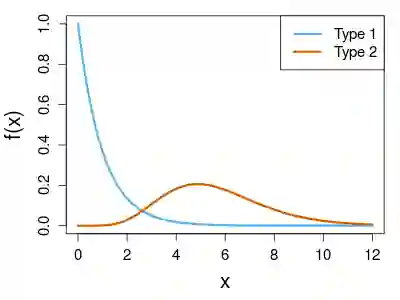
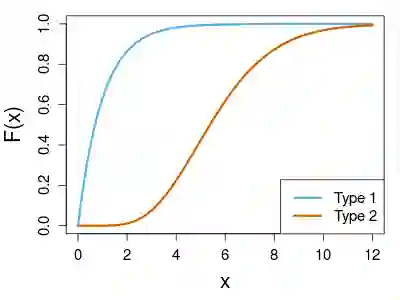
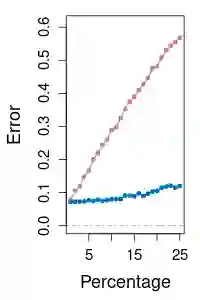
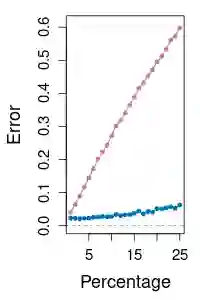
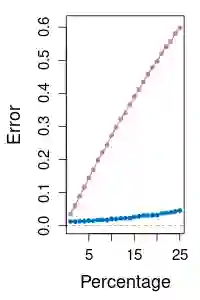
Measures of central tendency such as the mean and the median are a primary way to summarize a given collection of random objects. In the field of optimal transport, the Wasserstein barycenter corresponds to the Fr\'echet or geometric mean of a set of probability measures, which is defined as a minimizer of the sum of its squared distances to each element of the set when the order is 2. We present the Wasserstein median, an equivalent of the Fr\'echet median under the 2- Wasserstein metric, as a robust alternative to the barycenter. The Wasserstein median is shown to be well defined and exist under mild conditions. We also propose an algorithm that makes use of any established routine for the Wasserstein barycenter in an iterative manner and prove its convergence. Our proposal is validated with simulated and real data examples when the objects of interest are univariate distributions, centered Gaussian distributions, and discrete measures on regular grids.
翻译:在最佳运输领域,瓦森斯坦中枢与一套概率计量法的Fr\'echet或几何平均值相对应,被定义为在命令为2时将瓦森斯坦中位数与每组元素平方距离之和最小化。我们提出了瓦森斯坦中位数,相当于2-瓦森斯坦中位数下的Fr\'echet中位数,作为2-瓦西斯坦中标的有力替代物。瓦森斯坦中位数被证明是定义完善的,并且存在于温和条件下。我们还提议一种算法,以迭接的方式为瓦森斯坦中枢使用任何既定的例行程序,并证明其趋同性。我们的提议得到模拟和真实数据示例的验证,当对象为非象状分布、中心高斯的分布和正常电网上的离散测量时。