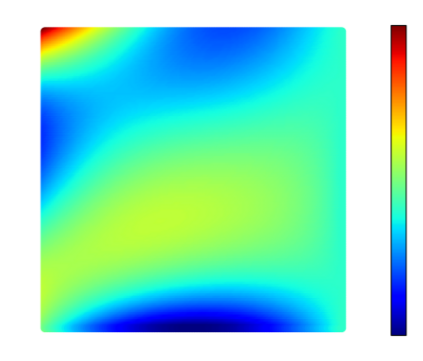
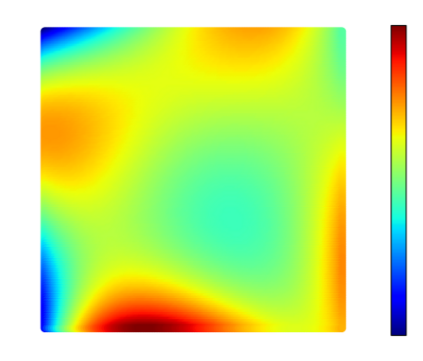
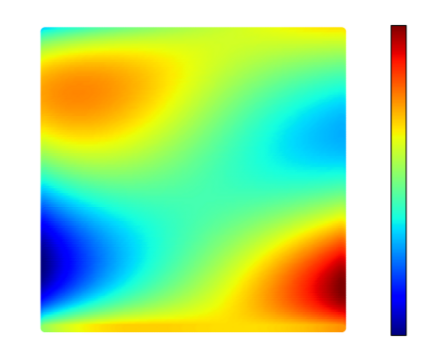
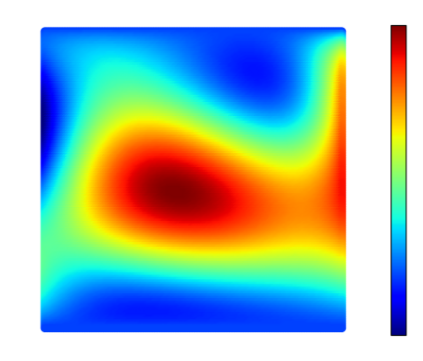
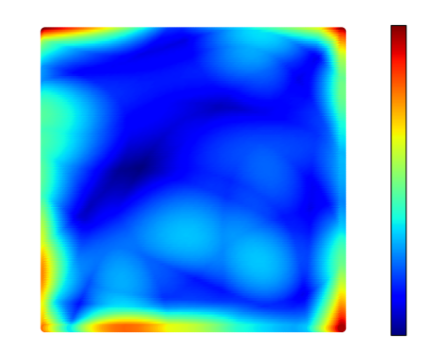
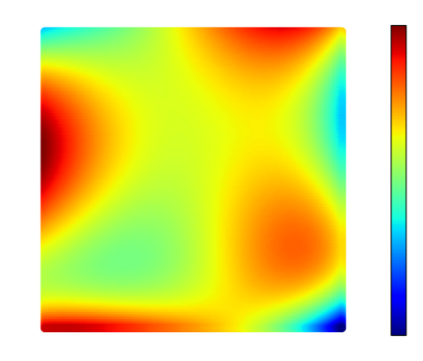
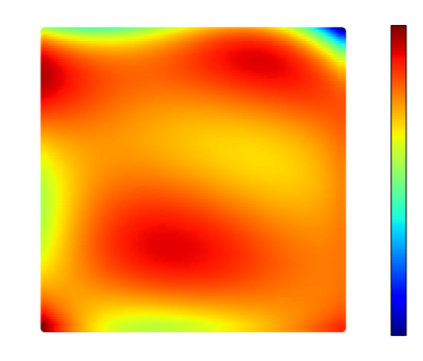
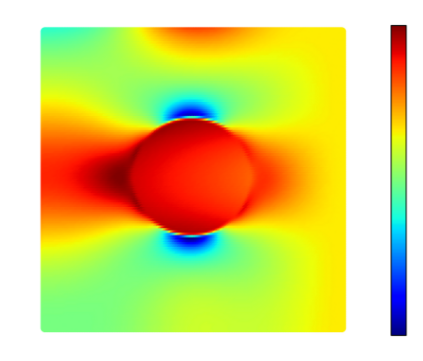
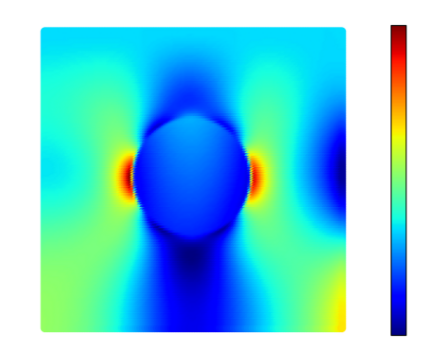
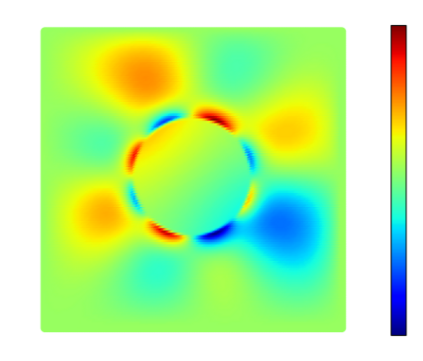
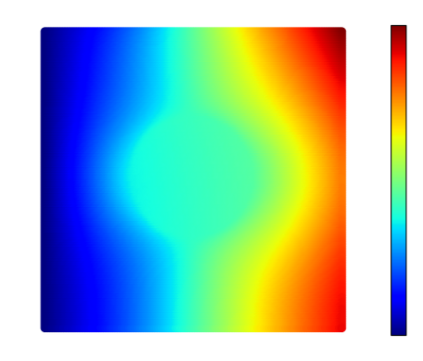
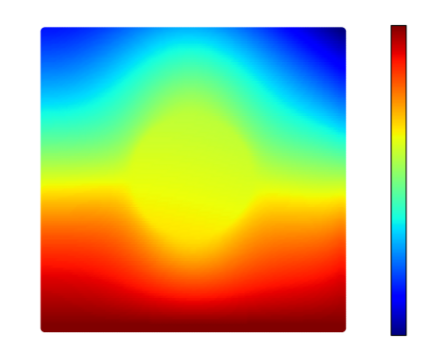
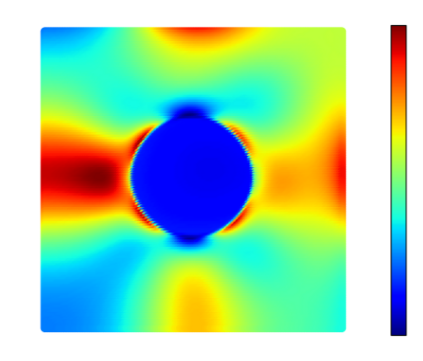
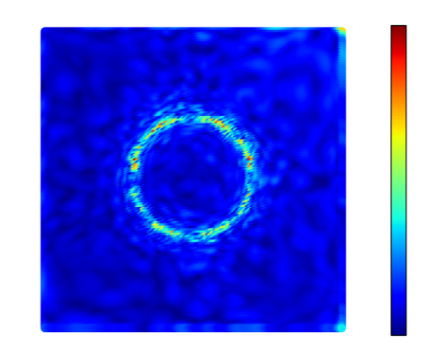
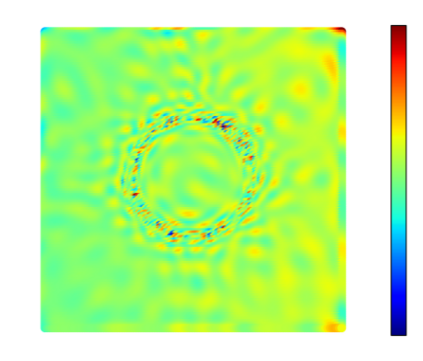
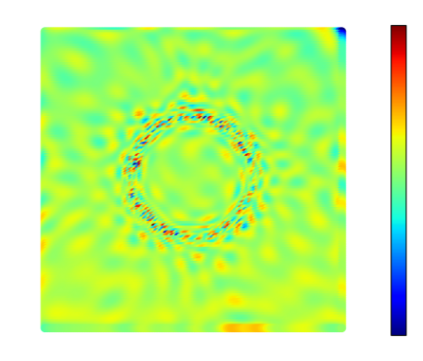
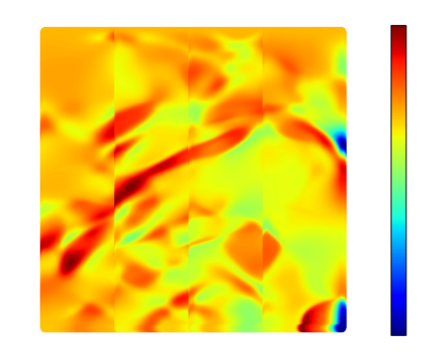
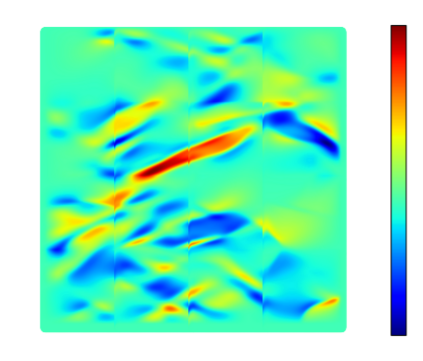
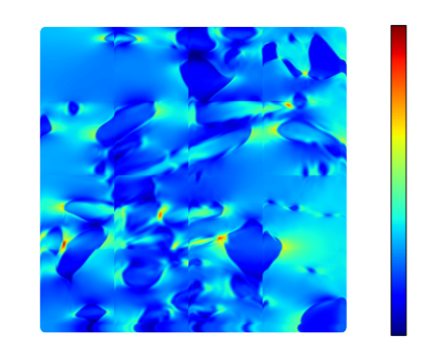
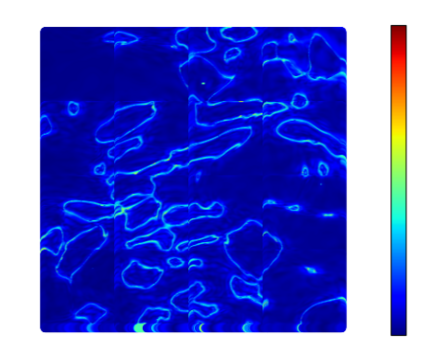
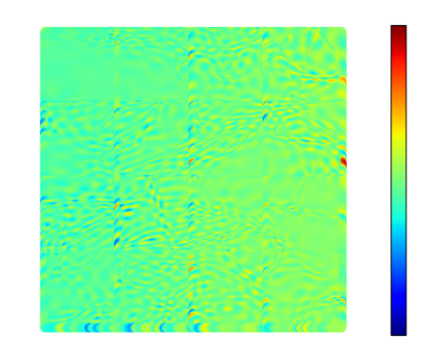
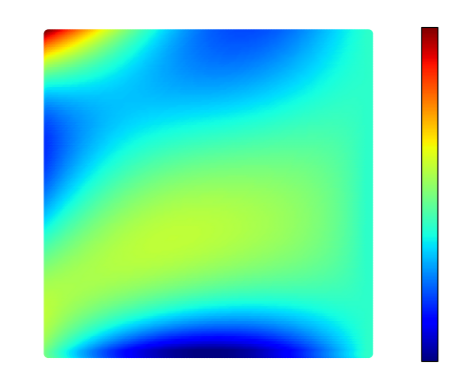
Recently, physics informed neural networks have successfully been applied to a broad variety of problems in applied mathematics and engineering. The principle idea is to use a neural network as a global ansatz function to partial differential equations. Due to the global approximation, physics informed neural networks have difficulties in displaying localized effects and strong non-linear solutions by optimization. In this work we consider material non-linearities invoked by material inhomogeneities with sharp phase interfaces. This constitutes a challenging problem for a method relying on a global ansatz. To overcome convergence issues, adaptive training strategies and domain decomposition are studied. It is shown, that the domain decomposition approach is able to accurately resolve nonlinear stress, displacement and energy fields in heterogeneous microstructures obtained from real-world $\mu$CT-scans.
翻译:最近,物理知情神经网络成功地应用于应用数学和工程方面的广泛问题,其主要思想是利用神经网络作为全球肛门功能,以部分差异方程式取代部分差异方程式。由于全球近似,物理知情神经网络难以通过优化显示局部效应和非线性解决方案。在这项工作中,我们考虑到与尖尖级界面有物质差异的物质不相容所引用的物质非线性。这对依赖全球炭疽系统的方法来说是一个具有挑战性的问题。为了克服趋同问题,正在研究适应性培训战略和域分解。显示,域分解法能够准确地解决从实际世界获得的美元/美元/美元/日元/日元空间的各种微结构中的非线性压力、迁移和能源领域。