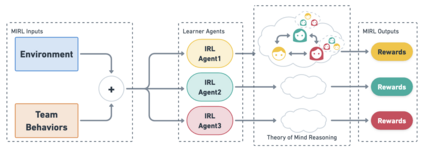
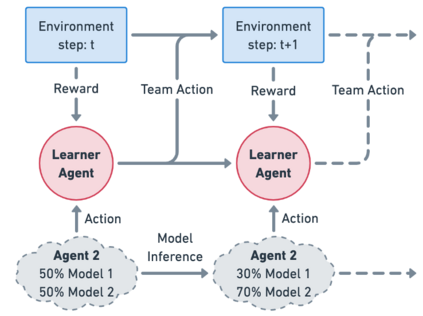
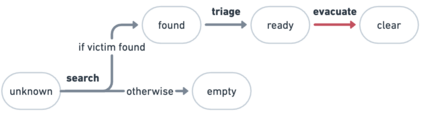
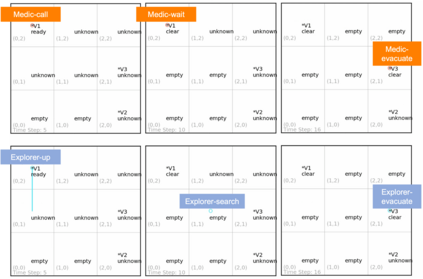
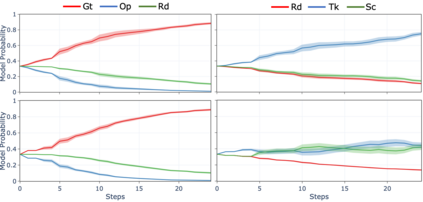
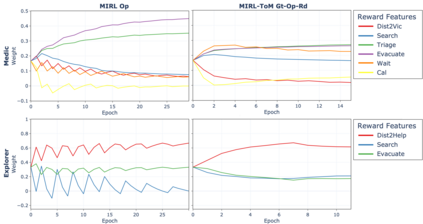
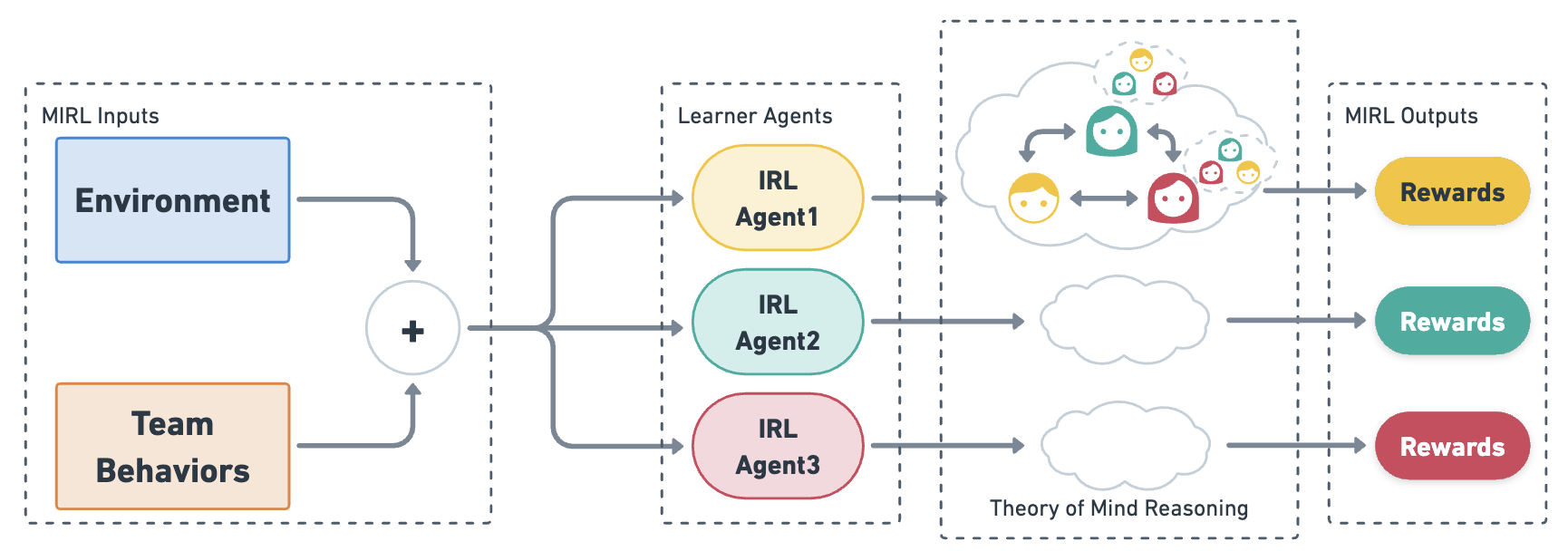
We approach the problem of understanding how people interact with each other in collaborative settings, especially when individuals know little about their teammates, via Multiagent Inverse Reinforcement Learning (MIRL), where the goal is to infer the reward functions guiding the behavior of each individual given trajectories of a team's behavior during some task. Unlike current MIRL approaches, we do not assume that team members know each other's goals a priori; rather, that they collaborate by adapting to the goals of others perceived by observing their behavior, all while jointly performing a task. To address this problem, we propose a novel approach to MIRL via Theory of Mind (MIRL-ToM). For each agent, we first use ToM reasoning to estimate a posterior distribution over baseline reward profiles given their demonstrated behavior. We then perform MIRL via decentralized equilibrium by employing single-agent Maximum Entropy IRL to infer a reward function for each agent, where we simulate the behavior of other teammates according to the time-varying distribution over profiles. We evaluate our approach in a simulated 2-player search-and-rescue operation where the goal of the agents, playing different roles, is to search for and evacuate victims in the environment. Our results show that the choice of baseline profiles is paramount to the recovery of the ground-truth rewards, and that MIRL-ToM is able to recover the rewards used by agents interacting both with known and unknown teammates.
翻译:与当前 MIRL 方法不同, 我们并不认为团队成员先天了解对方的目标; 相反, 他们合作的方式是适应他人通过观察自己的行为而看到的目标, 并且共同执行任务。 为了解决这个问题, 我们建议通过Mind Theory(MIRL-ToM)对 MIRL 采用新颖的方法。 对于每个代理, 我们首先使用 ToM 推理法来估计基线奖赏简介的后缀分布。 我们随后通过分散平衡, 使用单个代理最大 Etropy IRL 来推断每个代理的奖赏功能, 我们根据时间分布来模拟其他团队的行为。 为了解决这个问题, 我们通过Mind Theory(MIRL- ToM)对 MIRL 提出了一个新的方法。 对于每个代理, 我们首先使用ToM 推理法来估计基线奖赏简介中的后缀分布。 我们使用单一代理最大Entropy IRL 来显示每个代理的奖赏功能, 我们根据已知的时间分布来模拟其他团队的行为。 我们用模拟了我们模拟的MIL 方法, 复制第二角色搜索和最高奖赏 定位 显示我们最不为 的回收 的底级 的回收 目标, 用于我们的基准 的回收, 用于我们 的 的 搜索 的 的 的底底底值 显示为我们 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 目标 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的</s>