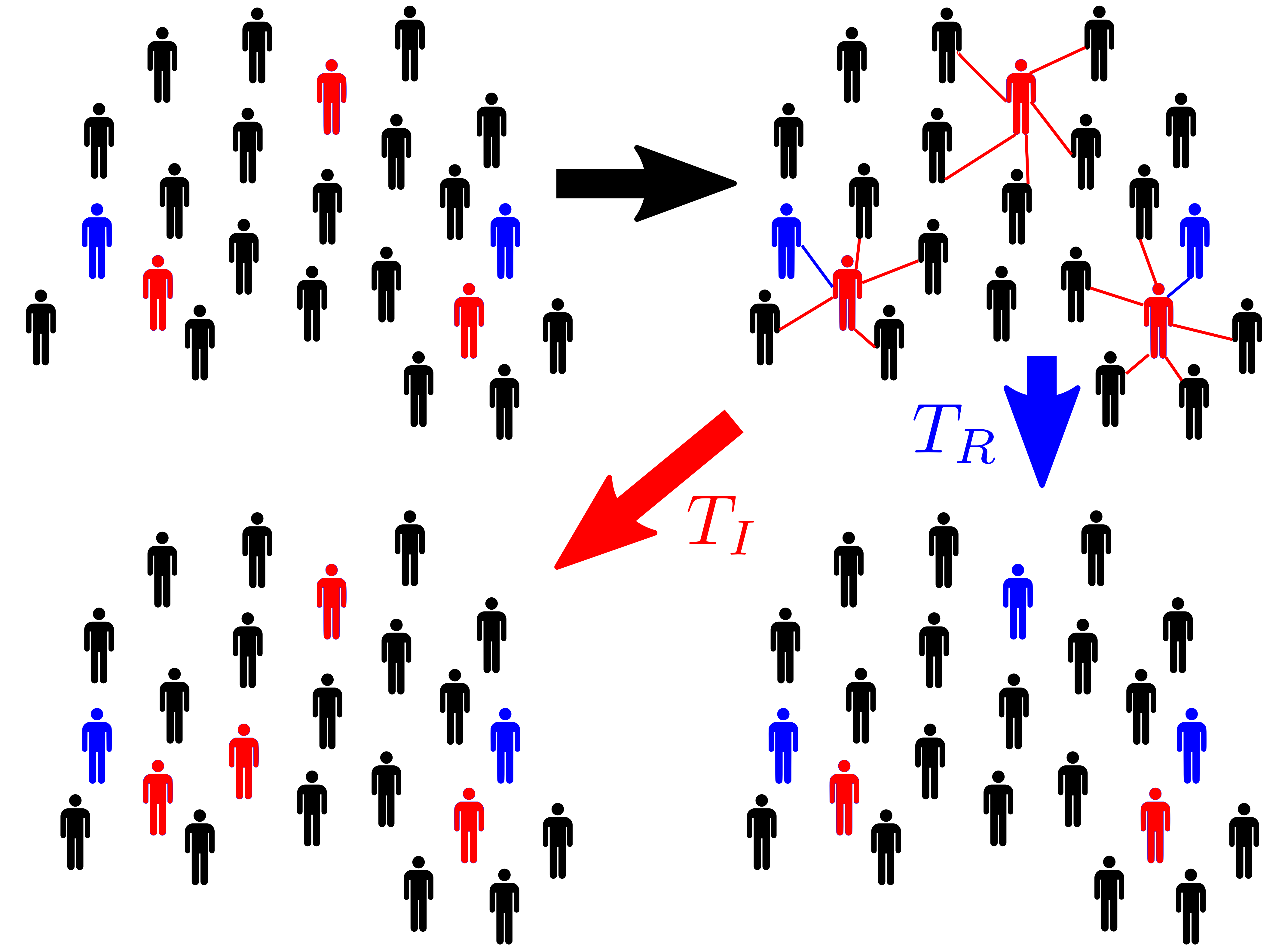
In the context of uncertainty quantification, computational models are required to be repeatedly evaluated. This task is intractable for costly numerical models. Such a problem turns out to be even more severe for stochastic simulators, the output of which is a random variable for a given set of input parameters. To alleviate the computational burden, surrogate models are usually constructed and evaluated instead. However, due to the random nature of the model response, classical surrogate models cannot be applied directly to the emulation of stochastic simulators. To efficiently represent the probability distribution of the model output for any given input values, we develop a new stochastic surrogate model called stochastic polynomial chaos expansions. To this aim, we introduce a latent variable and an additional noise variable, on top of the well-defined input variables, to reproduce the stochasticity. As a result, for a given set of input parameters, the model output is given by a function of the latent variable with an additive noise, thus a random variable. In this paper, we propose an adaptive algorithm which does not require repeated runs of the simulator for the same input parameters. The performance of the proposed method is compared with the generalized lambda model and a state-of-the-art kernel estimator on two case studies in mathematical finance and epidemiology and on an analytical example whose response distribution is bimodal. The results show that the proposed method is able to accurately represent general response distributions, i.e., not only normal or unimodal ones. In terms of accuracy, it generally outperforms both the generalized lambda model and the kernel density estimator.
翻译:在不确定性量化的背景下, 计算模型需要反复评估 。 对于昂贵的数值模型来说, 此任务很难解决 。 这样的问题对于随机模拟器来说甚至更为严重, 其输出是给定一组输入参数的随机变量。 为了减轻计算负担, 通常会构建并评估代孕模型。 但是, 由于模型反应的随机性质, 经典代金模型不能直接用于模拟随机模拟模拟器的模拟。 为了有效地代表模型输出对于任何特定输入值的精确度分布, 我们开发了一个叫做随机模拟模拟模拟模拟模拟模拟模型模型的模型, 其输出的精度甚至更为严重。 为了这个目的, 我们引入了一个潜伏变量和一个额外的噪声变量, 在定义明确的输入变量之上, 复制预设的代金模型。 对于一个输入参数来说, 模型输出只能由一个具有添加性噪音的潜值变量函数来提供, 因此随机变量。 在本文中, 我们建议一个适应性算算法, 不需要反复运行双向分析公式的公式, 以及两个分析参数的缩略图, 显示一个比法的缩缩缩图。