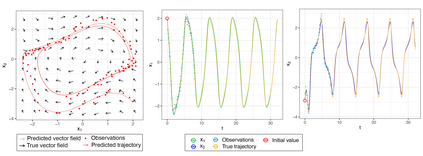
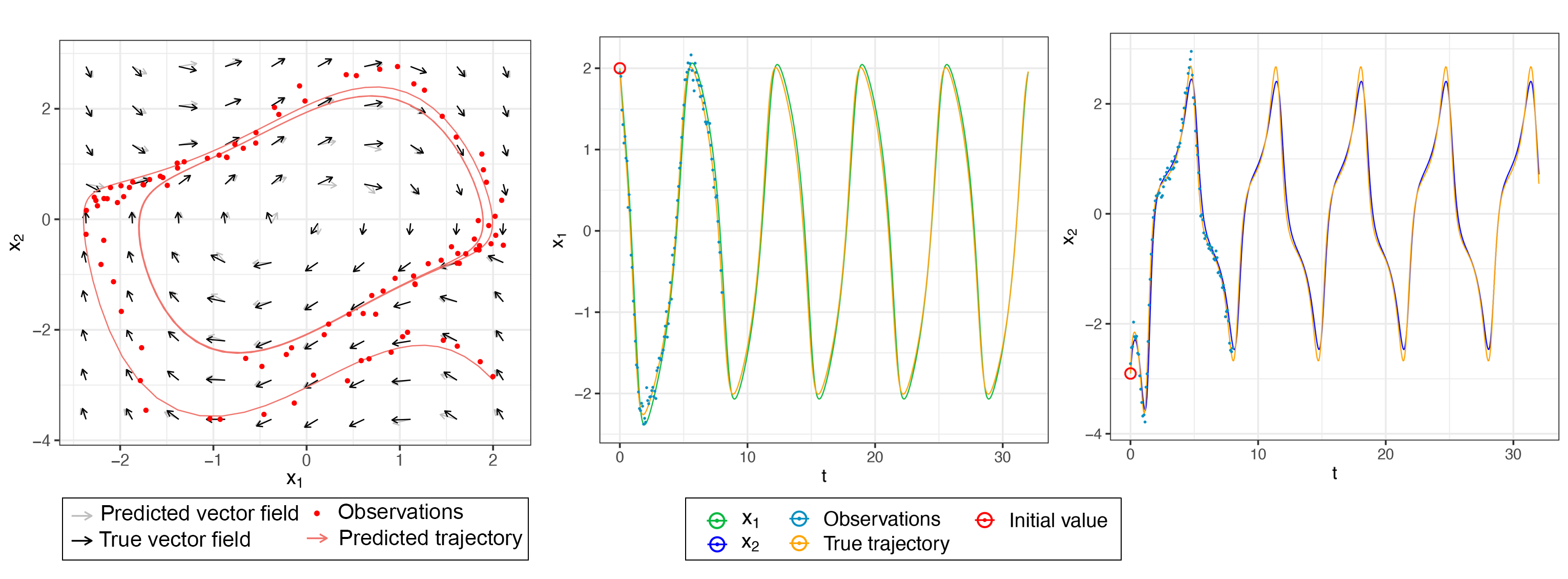
Learning Nonparametric Ordinary differential Equations: Application to Sparse and Noisy Data

Learning nonparametric systems of Ordinary Differential Equations (ODEs) $\dot x = f(t,x)$ from noisy and sparse data is an emerging machine learning topic. We use the well-developed theory of Reproducing Kernel Hilbert Spaces (RKHS) to define candidates for $f$ for which the solution of the ODE exists and is unique. Learning $f$ consists of solving a constrained optimization problem in an RKHS. We propose a penalty method that iteratively uses the Representer theorem and Euler approximations to provide a numerical solution. We prove a generalization bound for the $L^2$ distance between $x$ and its estimator. Experiments are provided for the FitzHugh Nagumo oscillator and for the prediction of the Amyloid level in the cortex of aging subjects. In both cases, we show competitive results when compared with the state of the art.