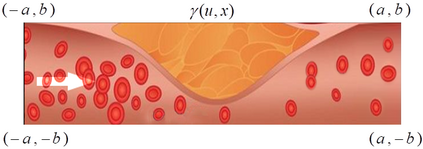
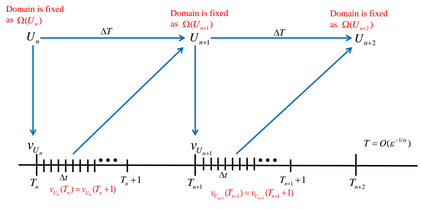
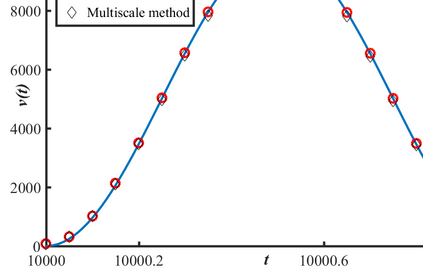
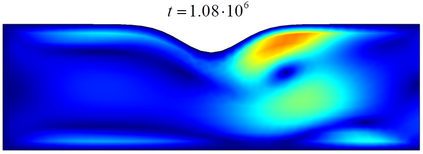
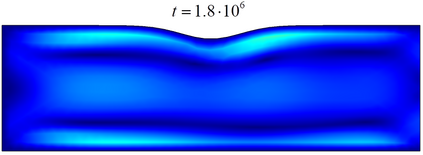
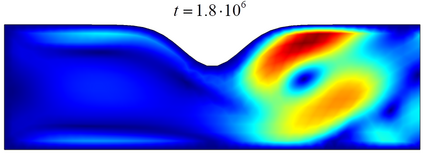
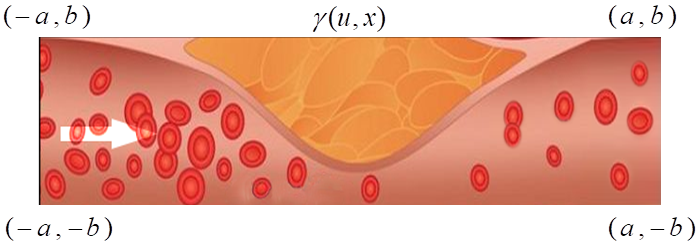
This paper is concerned with a blood flow problem coupled with a slow plaque growth at the artery wall. In the model, the micro (fast) system is the Navier-Stokes equation with a periodically applied force and the macro (slow) system is a fractional reaction equation, which is used to describe the plaque growth with memory effect. We construct an auxiliary temporal periodic problem and an effective time-average equation to approximate the original problem and analyze the approximation error of the corresponding linearized PDE (Stokes) system, where the simple front-tracking technique is used to update the slow moving boundary. An effective multiscale method is then designed based on the approximate problem and the front tracking framework. We also present a temporal finite difference scheme with a spatial continuous finite element method and analyze its temporal discrete error. Furthermore, a fast iterative procedure is designed to find the initial value of the temporal periodic problem and its convergence is analyzed as well. Our designed front-tracking framework and the iterative procedure for solving the temporal periodic problem make it easy to implement the multiscale method on existing PDE solving software. The numerical method is implemented by a combination of the finite element platform COMSOL Multiphysics and the mainstream software MATLAB, which significantly reduce the programming effort and easily handle the fluid-structure interaction, especially moving boundaries with more complex geometries. We present some numerical examples of ODEs and 2-D Navier-Stokes system to demonstrate the effectiveness of the multiscale method. Finally, we have a numerical experiment on the plaque growth problem and discuss the physical implication of the fractional order parameter.
翻译:本文关注血液流动问题,同时在动脉壁上缓慢增长。在模型中,微型(快)系统是带有定期应用力的纳维埃-斯托克斯方程式,而宏观(慢)系统是一个分反应方程式,用来描述带有记忆效果的红板增长。我们构建了一个辅助时间周期问题和有效时间平均方程式,以大致了解原始问题,并分析相应的线性PDE(斯托克斯)系统的近似差错,即使用简单的前跟踪技术来更新缓慢移动的边界。随后,根据近似问题和前跟踪框架设计了一个有效的多尺度方法。我们还提出了一个带有空间连续要素法的时性有限差异方程式,分析其时间性离散误差。此外,我们设计了一个快速的迭代方程式,以寻找时间周期问题的初步价值,并对解决时间性多周期问题的前跟踪框架和迭代程序进行近似差,从而便于在现有的PDE解动软件上实施多尺度方法。我们采用的数字性多尺度法方法,以空间持续不变要素元素的数值值为矩阵,我们运用了多层次模型,并用多种数字方法,我们运用了多数值系统,从而大大地将模型化了MAS- aximal-al-al-al-al-al-ILLLLLLLLLLLLLLLL 和ILLLLL 的计算模型的模型的模型的计算,我们运用了多种努力的计算方法,我们运用了多种动作法,我们运用了多种努力的计算方法,我们运用了多种方法,我们使用了多种方法,我们使用了多种方法,我们使用了多种方法,将了多种方法,我们使用了多种方法,我们使用了多种方法,将了多种方法,我们使用了多种方法,将了多种方法,用了多种方法,将了多种方法,将了多种方法,将了多种方法,用了多种方法,将了多种方法,将了多种方法,将了多种方法,用了多种方法,我们用了多种方法,我们使用了多种方法,我们用了多种方法,我们操作方法,用了多种方法,将了多种方法,将了多种方法,将了多种方法,将了多种方法,将了多种方法,并用的计算方法,并用多种方法,用了多种方法,用了多种方法,用