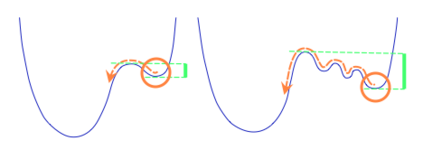
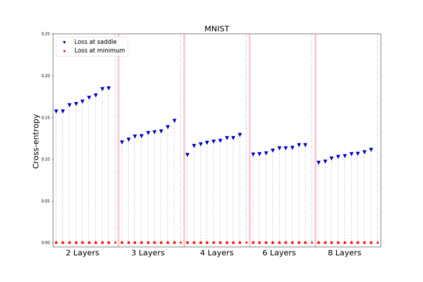
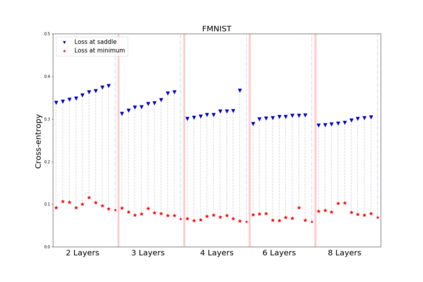
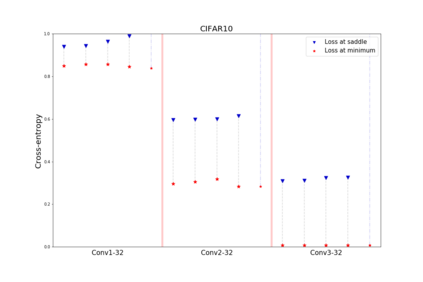
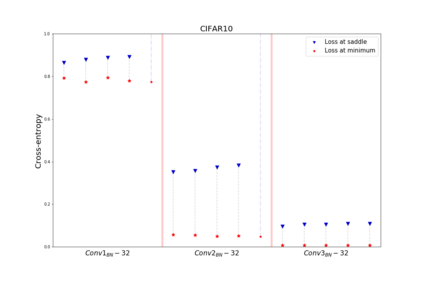
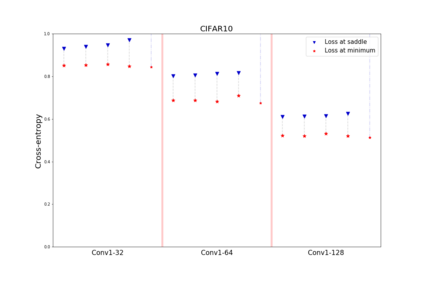
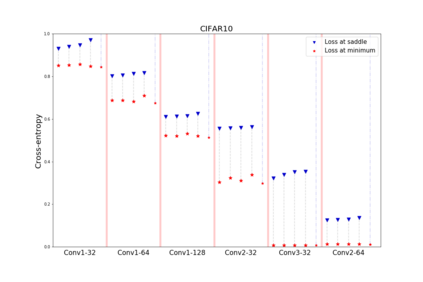
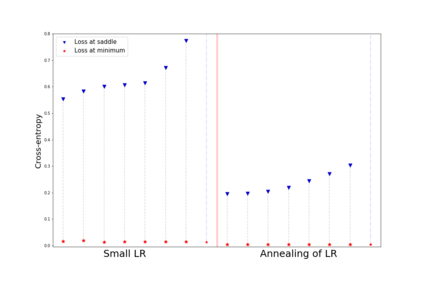
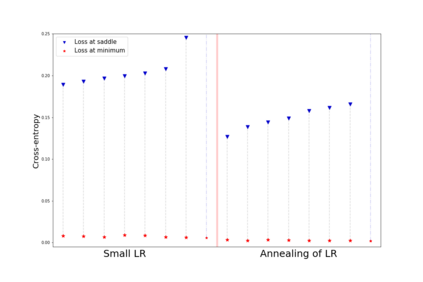
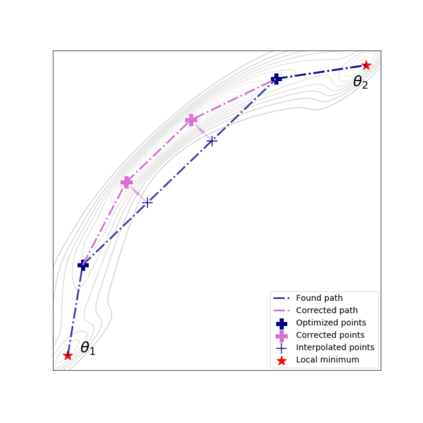
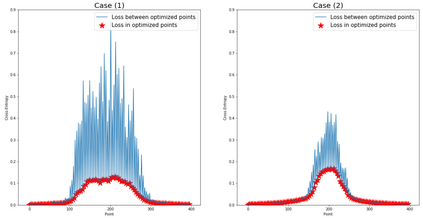
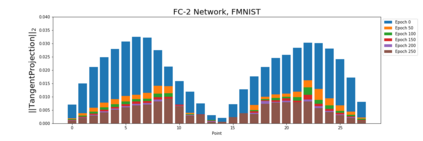
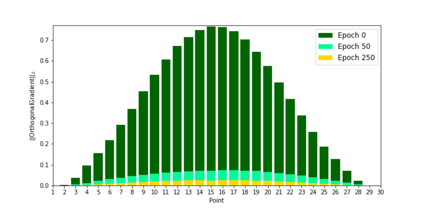
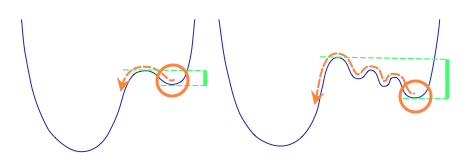
We apply methods of topological data analysis to loss functions to gain insights on learning of deep neural networks and their generalization properties. We study global properties of the loss function gradient flow. We use topological data analysis of the loss function and its Morse complex to relate local behavior along gradient trajectories with global properties of the loss surface. We define neural network Topological Obstructions score, TO-score, with help of robust topological invariants, barcodes of loss function, that quantify the badness of local minima for gradient-based optimization. We have made several experiments for computing these invariants, for small neural networks, and for fully connected, convolutional and ResNet-like neural networks on different datasets: MNIST, Fashion MNIST, CIFAR10, SVHN. Our two principal observations are as follows. Firstly, the neural network barcode and TO-score decrease with the increase of the neural network depth and width. Secondly, there is an intriguing connection between the length of minima segments in the barcode and the minima generalization error.
翻译:我们对损失功能应用了地形数据分析方法,以深入了解深神经网络及其一般特性的学习情况。我们研究了损失函数梯度流的全球特性。我们使用损失函数及其摩斯综合体的地形数据分析方法,将梯度轨迹的当地行为与损失表面的全球特性联系起来。我们定义了神经网络地形障碍评分(to-score),在坚固的地形变异分子的帮助下,对损失函数条形码进行了计算,以量化本地微粒的坏坏处,以便进行梯度优化。我们进行了数项实验,以计算这些变异物、小神经网络、以及不同数据集上完全连接的、进化的和ResNet的神经网络:MNIST、Fashon MNIST、CIFAR10、SVHN。我们的主要观察如下:首先,神经网络条形码和原子减少与神经网络深度和宽度的增加有关。第二,在条形和微宽度差中微小段的长度与微小一般错误之间有细的连接。