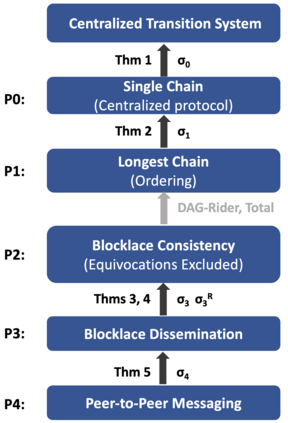
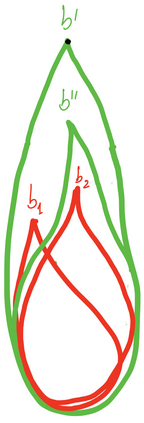
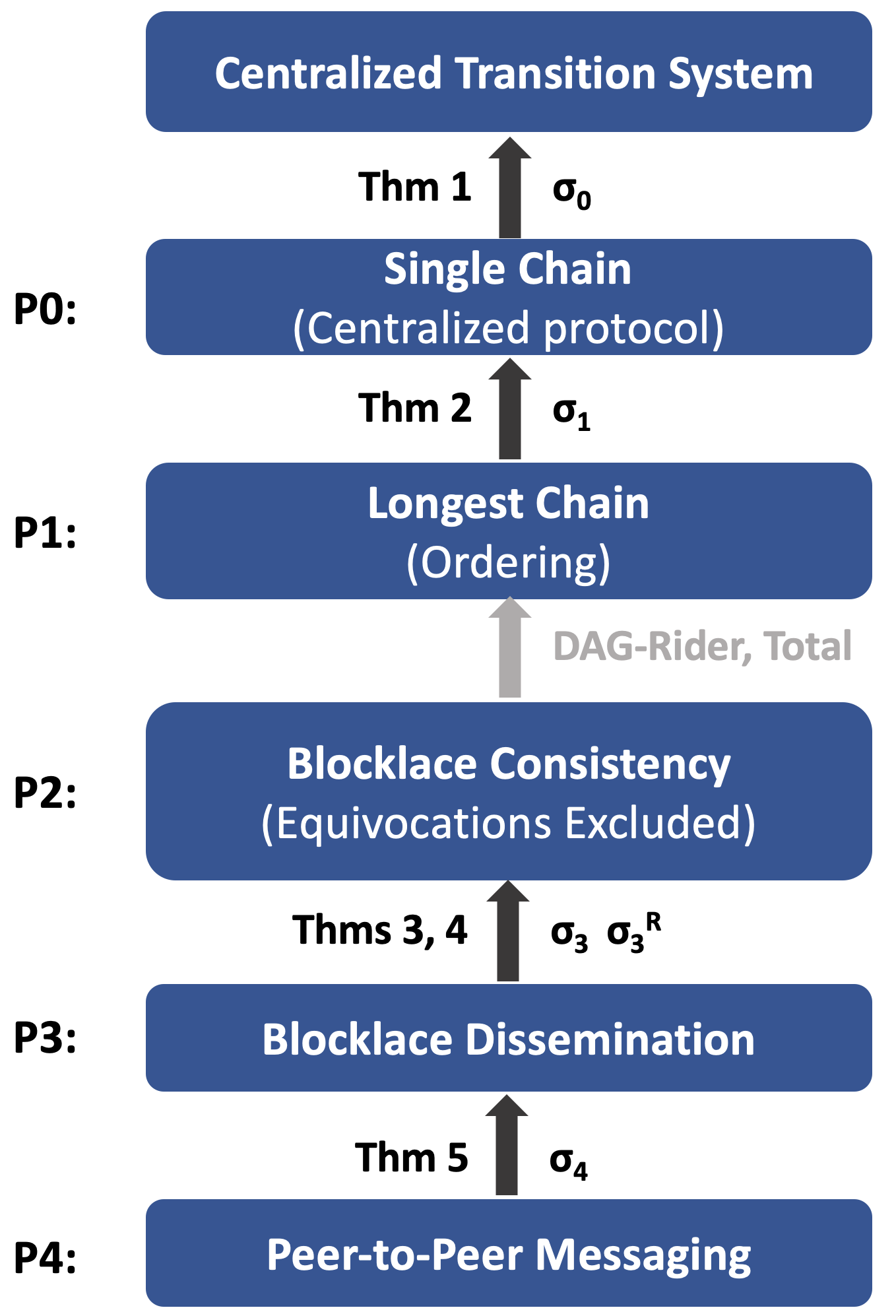
Presently, the practice of distributed computing is such that problems exist in a mathematical realm different from their solutions: a problem is presented as a set of requirements on possible process or system behaviors, and the solution is presented as algorithmic pseudocode satisfying the requirements. Here, we present a novel mathematical realm, termed \emph{multiagent transition systems}, that aims to accommodate both distributed computing problems and their solutions. A problem is presented as a specification -- a multiagent transition system -- and a solution as an implementation of the specification by another, lower-level multiagent transition systems. This duality of roles of a multiagent transition system can be exploited all the way from a high-level distributed computing problem description down to an agreed-upon base layer, say TCP/IP, resulting in a mathematical protocol stack where each protocol is implemented by the one below it. Correct implementations are compositional and thus provide also an implementation of the protocol stack as a whole. The framework also offers a formal, yet natural, notion of faults and their resilience. We present two illustrations of the power of the approach: A multiagent transition systems specifying a centralized single-chain protocol and a distributed longest-chain protocol, show an implementation of this protocol by the longest-chain protocol, and conclude -- via the compositionality of correct implementations -- that the distributed longest-chain protocol is universal for centralized multiagent transition systems. Second, we describe a DAG-based blockchain consensus protocol stack that addresses each of the key tasks of a blockchain protocol -- dissemination, equivocation-exclusion, and ordering -- by a different layer of the stack. Additional applications of this mathematical framework are underway.
翻译:目前,分布式计算的做法是,在数学领域存在不同于其解决办法的问题:一个问题作为一套关于可能的程序或系统行为的要求提出,一个问题作为一套关于可能的程序或系统行为的要求提出,而解决办法则作为符合要求的算法伪编码提出。在这里,我们提出了一个新的数学领域,称为\emph{多剂过渡系统},旨在兼顾分布式计算问题及其解决办法。一个问题作为一个规格 -- -- 多剂过渡系统 -- -- 以及作为另一个较低层次的多剂过渡系统执行规格的解决办法。多剂过渡系统的作用的双重性,可以从一个高层次的分布式计算应用到一个商定的基础层,如TCP/IP,由此产生了一个数学协议堆,其中每个协议都由下面的一个实施方执行。 正确的执行是构成性的,从而也提供了整个协议层的落实。这个框架还提供了一个正式的,但自然的缺陷及其复原力概念。我们通过两个关于方法的力量的图解:多剂过渡系统说明一个集中的单一链式协议,一个链式应用系统,一个我们通过协议执行最长时间的链式协议的版本,一个协议执行过程,一个最长时间的顺序,一个我们通过协议执行的链式协议的顺序,一个协议,一个最长时间的顺序,一个协议,一个协议执行系统,一个最长时间的顺序,一个协议的顺序,一个执行,一个协议的顺序,一个执行系统,一个最固定式的顺序。