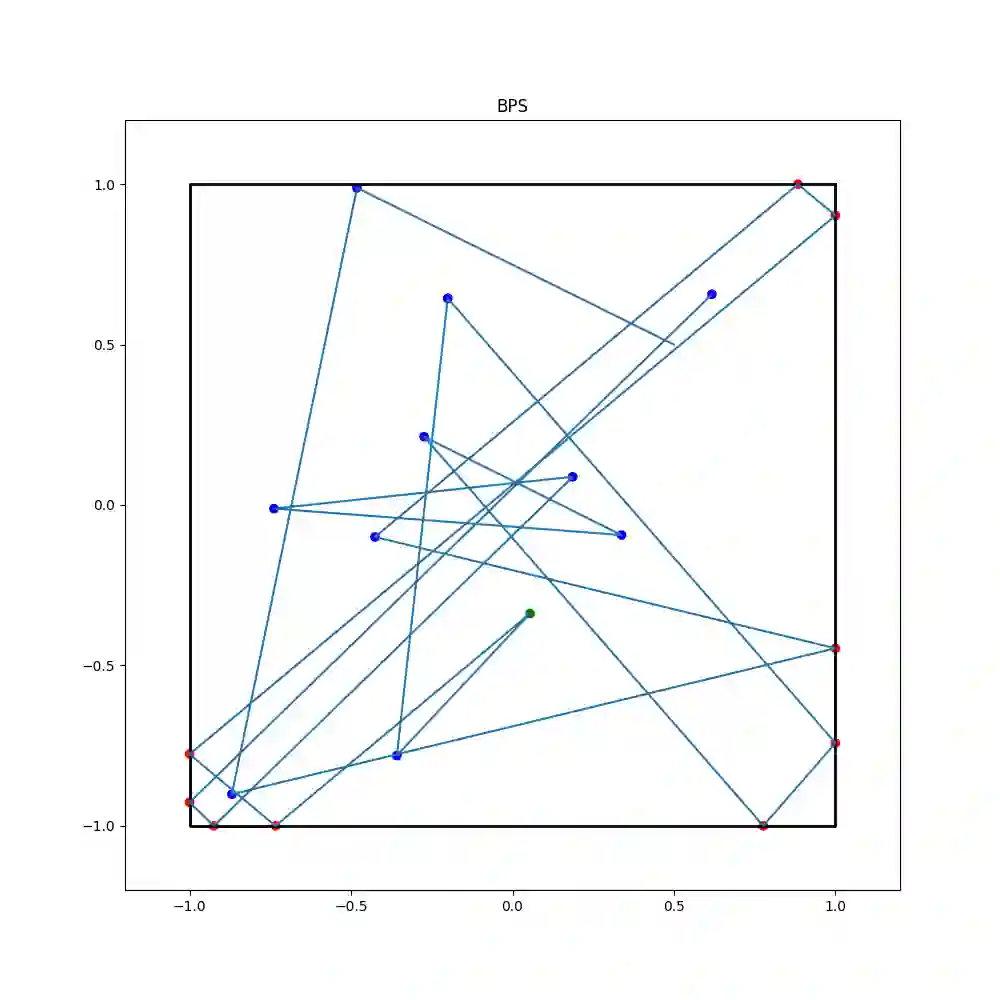
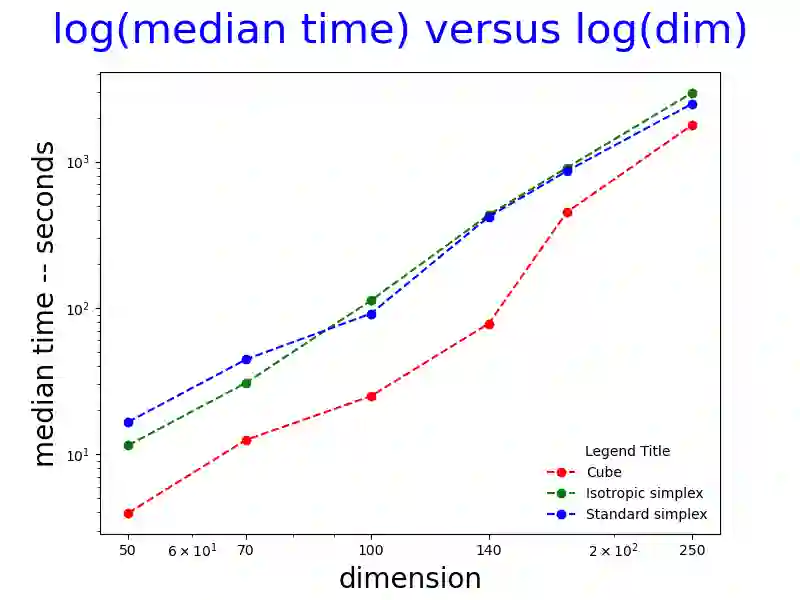
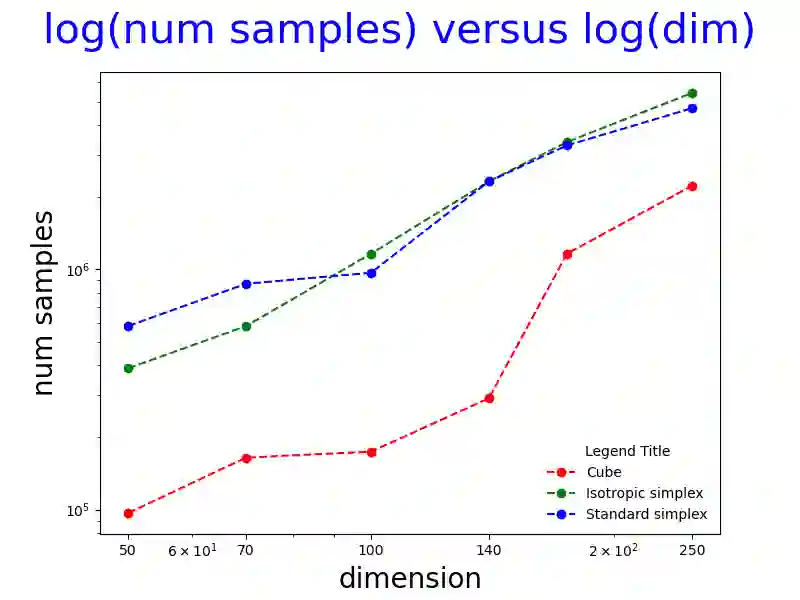
Computing the volume of a polytope in high dimensions is computationally challenging but has wide applications. Current state-of-the-art algorithms to compute such volumes rely on efficient sampling of a Gaussian distribution restricted to the polytope, using e.g. Hamiltonian Monte Carlo. We present a new sampling strategy that uses a Piecewise Deterministic Markov Process. Like Hamiltonian Monte Carlo, this new method involves simulating trajectories of a non-reversible process and inherits similar good mixing properties. However, importantly, the process can be simulated more easily due to its piecewise linear trajectories - and this leads to a reduction of the computational cost by a factor of the dimension of the space. Our experiments indicate that our method is numerically robust and is one order of magnitude faster (or better) than existing methods using Hamiltonian Monte Carlo. On a single core processor, we report computational time of a few minutes up to dimension 500.
翻译:计算高维的多管体积具有计算上的挑战性,但具有广泛的应用性。 计算这种体积的当前最先进的算法取决于对限制在多管体内的高斯分布的有效取样, 例如使用汉密尔顿·蒙特卡洛。 我们提出了一个新的抽样战略, 使用小的决定因素马克诺夫进程。 像汉密尔顿·蒙特卡洛一样, 这一新的方法涉及模拟不可逆过程的轨迹, 并继承类似的良好的混合特性。 但是, 重要的是, 这一过程可以更容易地模拟, 因为它的片断线性线性轨迹 - 这导致计算成本通过空间的维度来降低。 我们的实验表明, 我们的方法在数字上是稳健的, 比使用汉密尔顿· 蒙特卡洛的现有方法更快( 或更好 ) 。 在单一的核心处理器上, 我们报告计算时间数分钟到500维度。