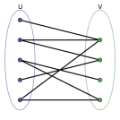
In this work, we focus on the Bipartite Stochastic Block Model (BiSBM), a popular model for bipartite graphs with a community structure. We consider the high dimensional setting where the number $n_1$ of type I nodes is far smaller than the number $n_2$ of type II nodes. The recent work of Braun and Tyagi (2022) established a sufficient and necessary condition on the sparsity level $p_{max}$ of the bipartite graph to be able to recover the latent partition of type I nodes. They proposed an iterative method that extends the one proposed by Ndaoud et al. (2022) to achieve this goal. Their method requires a good enough initialization, usually obtained by a spectral method, but empirical results showed that the refinement algorithm doesn't improve much the performance of the spectral method. This suggests that the spectral achieves exact recovery in the same regime as the refinement method. We show that it is indeed the case by providing new entrywise bounds on the eigenvectors of the similarity matrix used by the spectral method. Our analysis extend the framework of Lei (2019) that only applies to symmetric matrices with limited dependencies. As an important technical step, we also derive an improved concentration inequality for similarity matrices.
翻译:本文研究二分随机块模型 (BiSBM),这是一种带有社区结构的常见二分图模型。我们考虑一个高维设置,即节点类型 I 的数量 $n_1$ 明显小于节点类型 II 的数量 $n_2$。Braun 和 Tyagi(2022)最近提出了一个关于二分图稀疏度 $p_{max}$ 的充分必要条件,以便能够恢复类型 I 节点的潜在分区。他们提出了一种迭代方法来实现这个目标。该方法需要良好的初始化,通常是通过谱方法得到的,但实验结果表明精细算法并没有显著提高谱方法的性能。这表明谱方法能够在相同的恢复区间内实现精确恢复。我们通过提供相似矩阵的特征向量的新逐项界限,验证了这一点。我们的分析扩展了 Lei (2019) 的框架,后者仅适用于具有有限依赖性的对称矩阵。作为一个重要的技术步骤,我们还导出了一种改进的相似矩阵浓度界限。