Neural Eigenmap: 基于谱学习的结构化表示学习

©作者 | 邓志杰

单位 | 上海交通大学助理教授

我们在 Neural Eigenmaps paper 中 revisit 了表示学习的 eigenmap 原则。

论文标题：

Neural Eigenfunctions Are Structured Representation Learners

论文链接：

https://arxiv.org/pdf/2210.12637.pdf

代码链接：

https://github.com/thudzj/NEigenmaps

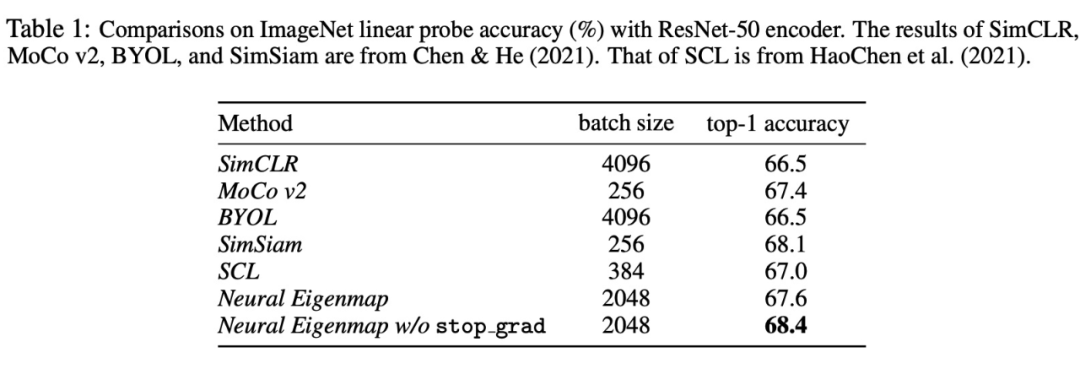
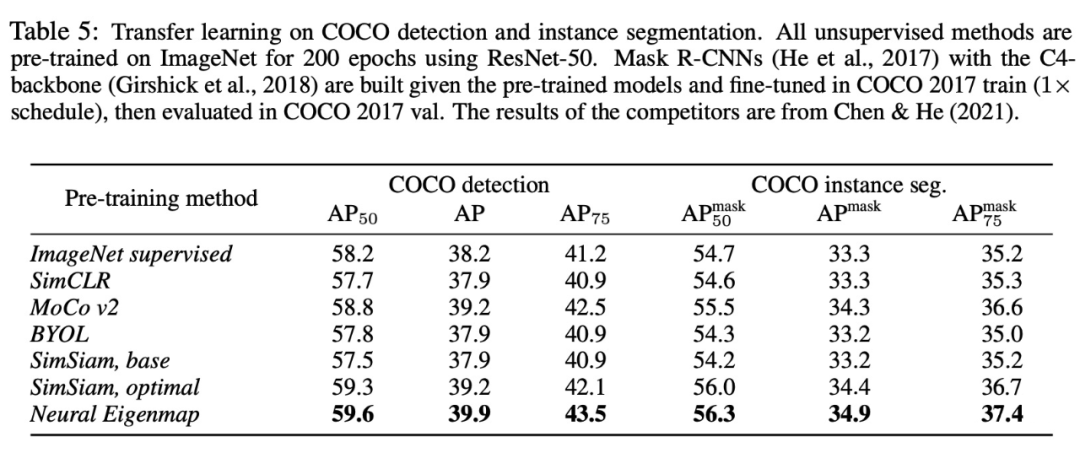
我们从理论上为包括但不限于 Barlow Twins 等方法提供了谱学习角度的解释以及修正，实验结果很有竞争力：

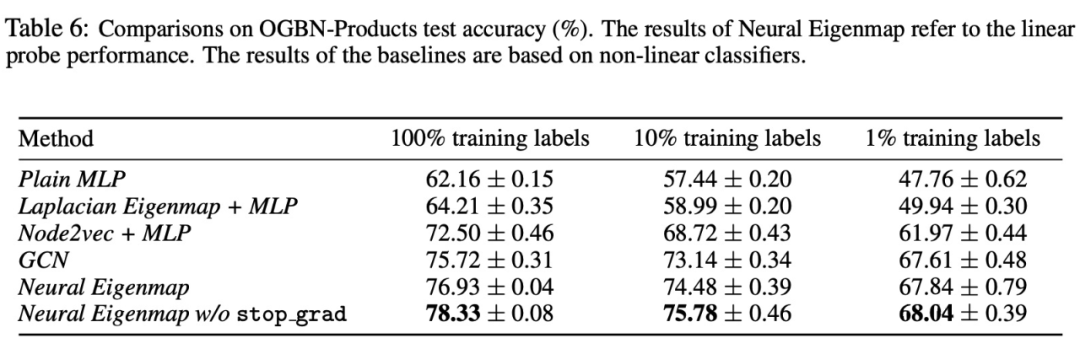
表示学习的eigenmap原则

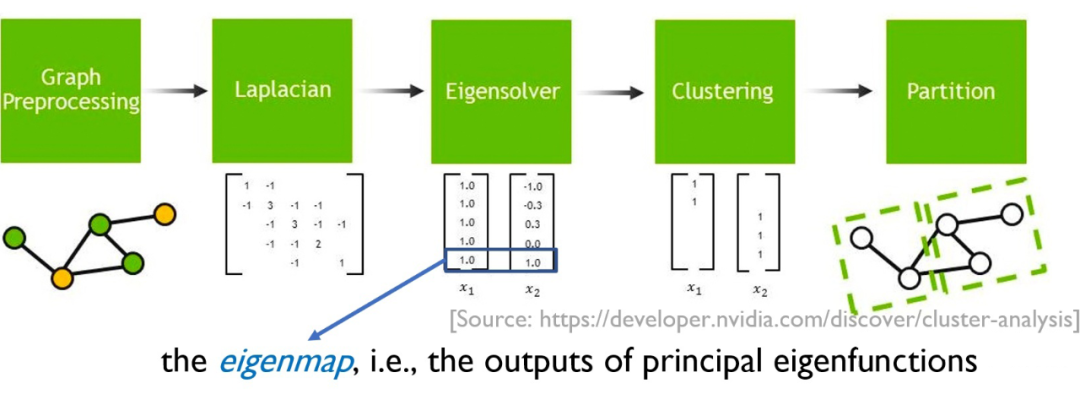
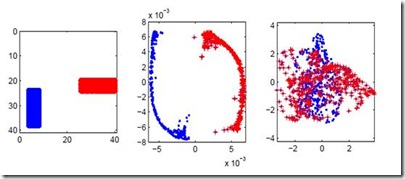
Eigenmaps 是特征函数（eigenfunctions）的输出。Eigenmaps 和表示学习的密切关联可以回溯到 spectral clustering [Shi & Malik, 2000] 和 Laplacian Eigenmaps [Belkin & Niyogi, 2003]：

▲ Laplacian Eigenmaps

这些方法基于图邻接矩阵（graph adjacency matrix）定义一个核，计算其主特征函数，并以其输出作为节点的表示，完成后续的聚类等任务。上述 Eigenmaps 是谱学习中的核心概念，也被证明是能够维持数据流形上的局部邻域结构的最优表示。

自监督设定下的核函数

自监督学习中，我们训练神经网络最大化同一数据的不同扰动版本在输出空间的相似度。

▲ 自监督学习最大化输出空间中同一样本的不同扰动间的相似度

Johnson et al. [2022] 证明，这种学习方式隐式地设定了一个参数化的核函数，其会收敛到半正定的对比核函数（contrastive kernel），定义如下

其中， 表示原始干净数据的分布， 表示随机扰动对应的分布。这个核函数的定义也和 HaoChen et al. [2021] 的群体增广图（population augmentation graph）有密切关联。直观上， 能够反映两个增广数据点来源于同一个原始样本的概率，因此可以反映它们之间的语义接近程度或内在相似性。

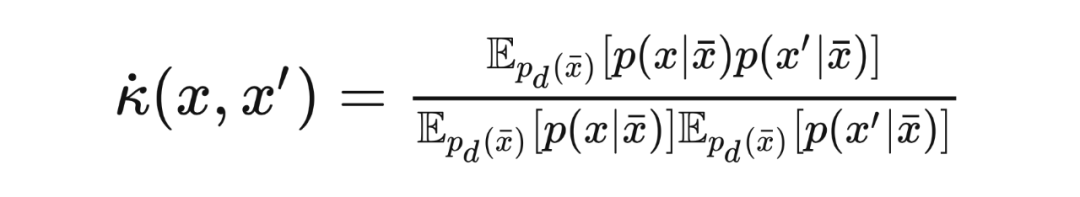
用神经网络近似核的主特征函数

Spectral clustering 和 Laplacian Eigenmaps 是非参的，依赖于求解一个矩阵特征值问题得到 eigenmaps，不能拓展到大规模训练数据上，也不能高效地执行样本外泛化。我们开发了参数化的方法来解决此问题：用神经网络作为函数逼近器来近似核函数的主特征函数。

虽然这个想法很简单，直到最近这件事才变得高效可行——首先是 Pfau et al. [2018] 的 SpIN，然后是我们的 ICML paper NeuralEF。NeuralEF 以比 SpIN 更简单的方式，保证 k 个主特征函数间的正交性，也避免了对雅可比矩阵的存储更新。它通过同时解 k 个非对称的优化问题来训练深度网络逼近 k 个主特征函数。在新的 paper，我们进一步推广了 NeuralEF 以允许权重共享和处理非正定核函数。

Neural Eigenmaps

定义一个 k 输出的神经网络作为 k 个主特征函数的逼近器，将对比核函数 带入上述非对称优化问题，即可得到一个新的、有理论保证的表示学习范式——Neural Eigenmaps。和自监督学习的常见方法例如 Barlow Twins 的直观对比如下：

▲ 现有自监督学习方法和Neural Eigenmaps的对比（具体loss的推导请参见我们的paper）

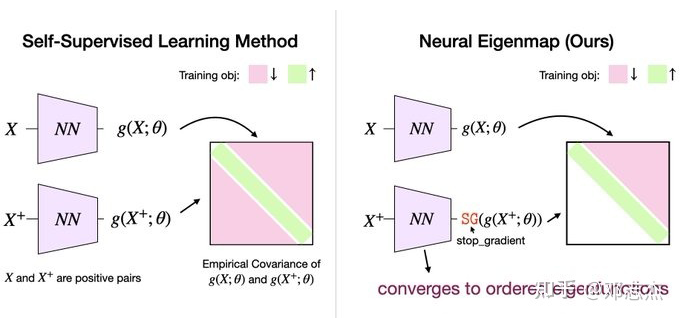
基于特定的 breaking-symmetry 手段（stop gradient 和仅优化上三角部分），Neural Eigenmaps 中神经网络的输出是结构化的，会逐元素收敛到核的 k 个主特征函数。

从这个意义上讲，Neural Eigenmaps 中元素的位置（index）是可以反映出其重要性程度的：index 更小的元素收敛到更主要的特征函数，所以包含更多来自原核函数的信息，因此更加重要。基于这样的结构，我们可以很灵活的在下游任务中通过对表示进行 truncation 实现 cost-quality tradeoff。

我们在迁移性的图像检索这个任务中验证了我们学得的表示中的这种结构：

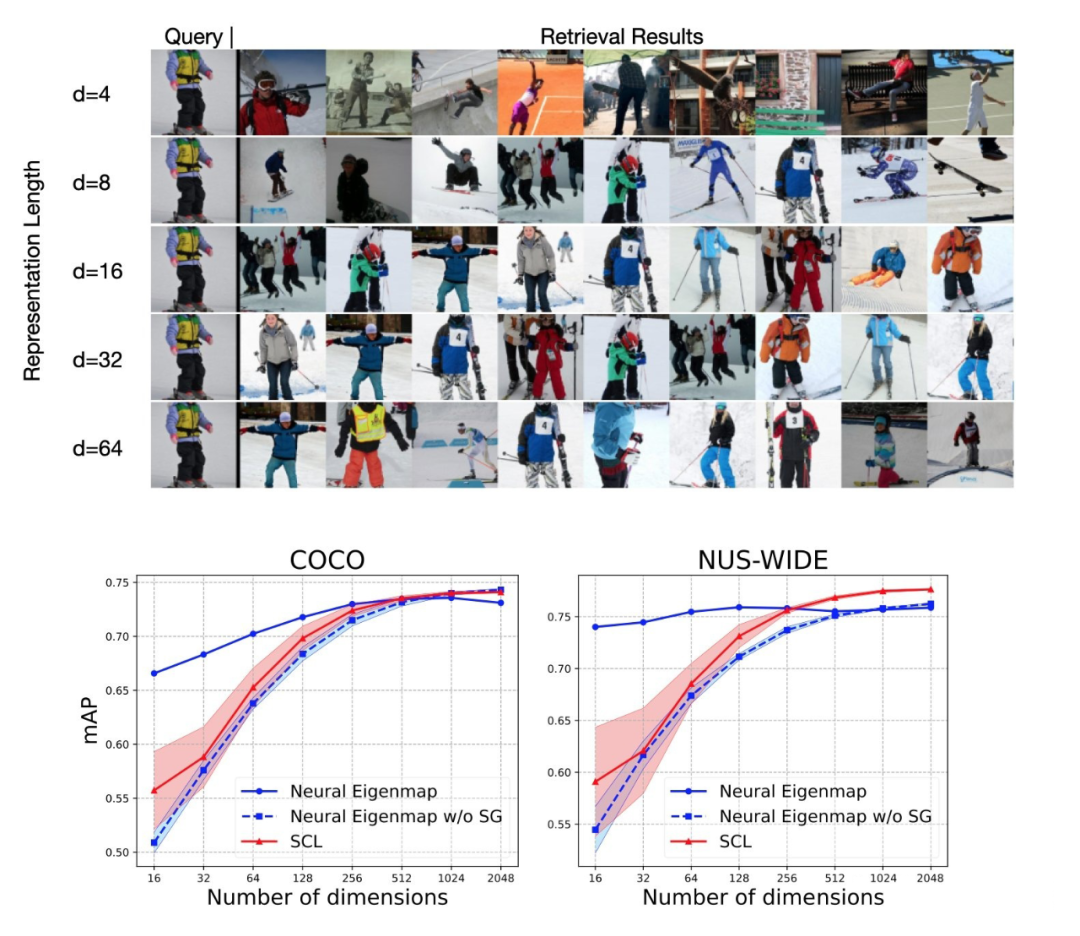
相比于现有方法，Neural Eigenmaps可以实现在不显著降低检索性能的情况下，减少至多94%的表示长度，这对于资源有限的应用场景十分重要。

最后

如果大家对 Neural Eigenmaps 感兴趣，欢迎试用我们的代码（目前开源还做的不是很好，欢迎感兴趣的同学参与进来，我的邮箱是 zhijied@sjtu[dot]edu[dot]cn）。

目前 Neural Eigenmaps 已被应用在自监督学习，图节点表示学习和谱聚类上，我们相信还有更多有想象力的应用场景值得探索。

更多阅读

#投 稿 通 道#

 让你的文字被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学术热点剖析、科研心得或竞赛经验讲解等。我们的目的只有一个，让知识真正流动起来。

📝 稿件基本要求：

• 文章确系个人原创作品，未曾在公开渠道发表，如为其他平台已发表或待发表的文章，请明确标注 

• 稿件建议以 markdown 格式撰写，文中配图以附件形式发送，要求图片清晰，无版权问题

• PaperWeekly 尊重原作者署名权，并将为每篇被采纳的原创首发稿件，提供业内具有竞争力稿酬，具体依据文章阅读量和文章质量阶梯制结算

📬 投稿通道：

• 投稿邮箱：hr@paperweekly.site 

• 来稿请备注即时联系方式（微信），以便我们在稿件选用的第一时间联系作者

• 您也可以直接添加小编微信（pwbot02）快速投稿，备注：姓名-投稿

△长按添加PaperWeekly小编

🔍

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

·