FinNet: Solving Time-Independent Differential Equations with Finite Difference Neural Network

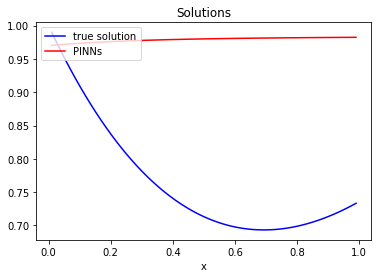
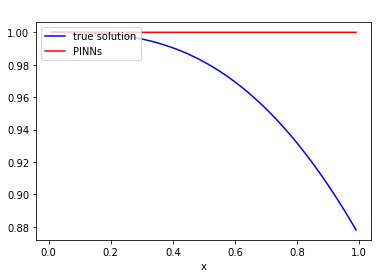
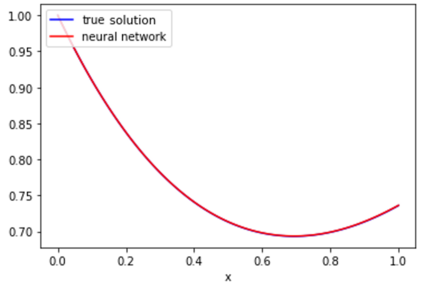
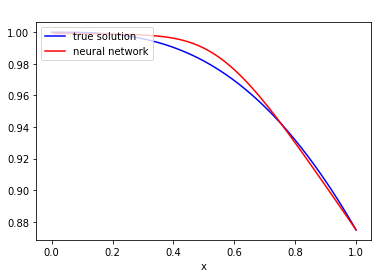
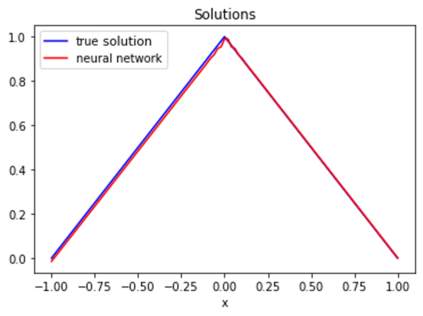
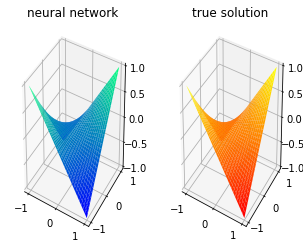
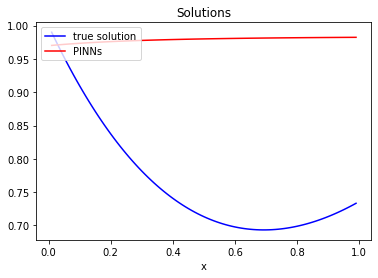
In recent years, deep learning approaches for partial differential equations have received much attention due to their mesh-freeness and other desirable properties. However, most of the works so far concentrated on time-dependent nonlinear differential equations. In this work, we analyze potential issues with the well-known Physic Informed Neural Network for differential equations that are not time-dependent. This analysis motivates us to introduce a novel technique, namely FinNet, for solving differential equations by incorporating finite difference into deep learning. Even though we use a mesh during the training phase, the prediction phase is mesh-free. We illustrate the effectiveness of our method through experiments on solving various equations.