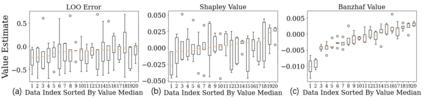
This paper studies the robustness of data valuation to noisy model performance scores. Particularly, we find that the inherent randomness of the widely used stochastic gradient descent can cause existing data value notions (e.g., the Shapley value and the Leave-one-out error) to produce inconsistent data value rankings across different runs. To address this challenge, we first pose a formal framework within which one can measure the robustness of a data value notion. We show that the Banzhaf value, a value notion originated from cooperative game theory literature, achieves the maximal robustness among all semivalues -- a class of value notions that satisfy crucial properties entailed by ML applications. We propose an algorithm to efficiently estimate the Banzhaf value based on the Maximum Sample Reuse (MSR) principle. We derive the lower bound sample complexity for Banzhaf value approximation, and we show that our MSR algorithm's sample complexity nearly matches the lower bound. Our evaluation demonstrates that the Banzhaf value outperforms the existing semivalue-based data value notions on several downstream ML tasks such as learning with weighted samples and noisy label detection. Overall, our study suggests that when the underlying ML algorithm is stochastic, the Banzhaf value is a promising alternative to the semivalue-based data value schemes given its computational advantage and ability to robustly differentiate data quality.
翻译:本文研究了数据估值对于吵闹模型性能评分的稳健性。 特别是,我们发现,广泛使用的随机性梯度梯度梯度下降的固有随机性可导致现有数据价值概念(例如,沙普利值和放出一差差差差差差差)产生不同运算的数据价值排名不一致。 为了应对这一挑战,我们首先提出一个正式框架,在这个框架内,人们可以测量数据价值概念的稳健性。我们显示,Banzhaf值,一种源自合作游戏理论文献的价值概念,在所有半值之间实现最强的稳健性 -- -- 一种满足ML应用程序关键特性的价值概念类别。我们提出一种算法,以便根据最大样品再利用原则高效估计Banzaf值值。我们得出Banzaf值接近值的低约束性抽样复杂性,我们表明,我们的MSR算法的精度复杂性几乎等于较低约束值。 我们的评估表明,Banzhaf值比现有的半值数据价值概念更符合若干下游ML任务,例如学习加权样品和焦标签检测等关键特性。 我们提出的算算, 当Banzh 的替代数据具有具有可靠的计算优势时,我们的研究显示, 当它具有具有具有可靠的模型的准性能的基值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值值为Banz- 。