Neural Network Approach to Stochastic Dynamics for Smooth Multimodal Density Estimation

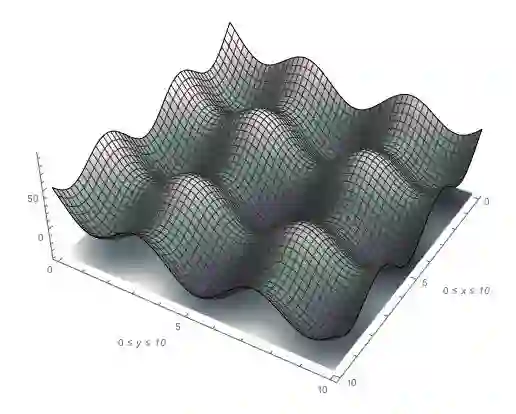
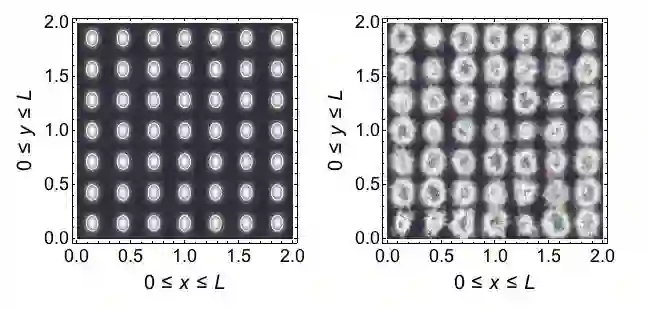
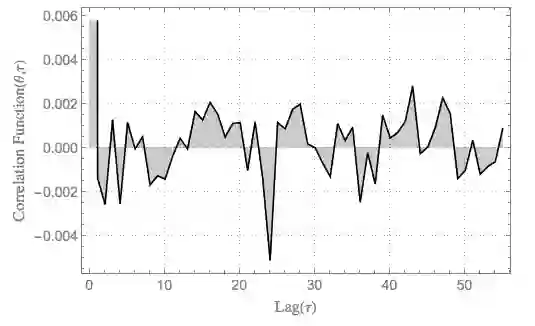
In this paper we consider a new probability sampling methods based on Langevin diffusion dynamics to resolve the problem of existing Monte Carlo algorithms when draw samples from high dimensional target densities. We extent Metropolis-Adjusted Langevin Diffusion algorithm by modelling the stochasticity of precondition matrix as a random matrix. An advantage compared to other proposal method is that it only requires the gradient of log-posterior. The proposed method provides fully adaptation mechanisms to tune proposal densities to exploits and adapts the geometry of local structures of statistical models. We clarify the benefits of the new proposal by modelling a Quantum Probability Density Functions of a free particle in a plane (energy Eigen-functions). The proposed model represents a remarkable improvement in terms of performance accuracy and computational time over standard MCMC method.