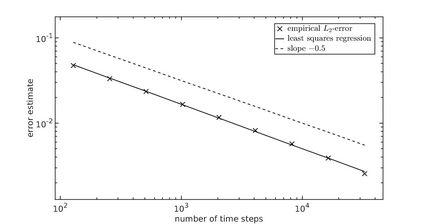
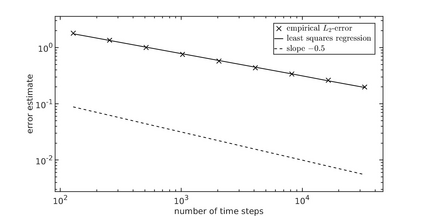
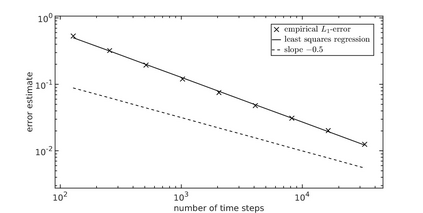
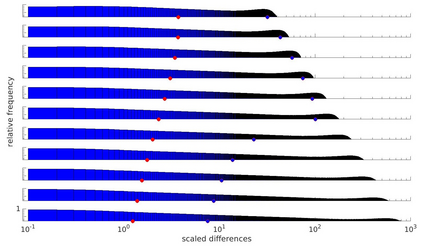
We study strong approximation of $d$-dimensional stochastic differential equations (SDEs) with a discontinuous drift coefficient. More precisely, we essentially assume that the drift coefficient is piecewise Lipschitz continuous with an exceptional set $\Theta\subset \mathbb{R}^d$ that is an orientable $C^4$-hypersurface of positive reach, the diffusion coefficient is assumed to be Lipschitz continuous and, in a neighborhood of $\Theta$, both coefficients are bounded and the diffusion coefficient has a non-degenerate portion orthogonal to $\Theta$. In recent years, a number of results have been proven in the literature for strong approximation of such SDEs and, in particular, the performance of the Euler-Maruyama scheme was studied. For $d=1$ and finite $\Theta$ it was shown that the Euler-Maruyama scheme achieves an $L_p$-error rate of at least $1/2$ for all $p\geq 1$ as in the classical case of Lipschitz continuous coefficients. For $d>1$, it was only known so far, that the Euler-Maruyama scheme achieves an $L_2$-error rate of at least $1/4-$ if, additionally, the coefficients $\mu$ and $\sigma$ are globally bounded. In this article, we prove that in the above setting the Euler-Maruyama scheme in fact achieves an $L_{p}$-error rate of at least $1/2-$ for all $d\in\mathbb{N}$ and all $p\geq 1$. The proof of this result is based on the well-known approach of transforming such an SDE into an SDE with globally Lipschitz continuous coefficients, a new It\^{o} formula for a class of functions which are not globally $C^2$ and a detailed analysis of the expected total time that the actual position of the time-continuous Euler-Maruyama scheme and its position at the preceding time point on the underlying grid are on 'different sides' of the hypersurface $\Theta$.
翻译:暂无翻译