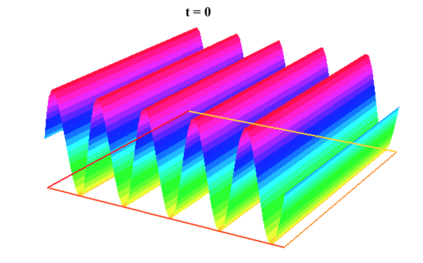
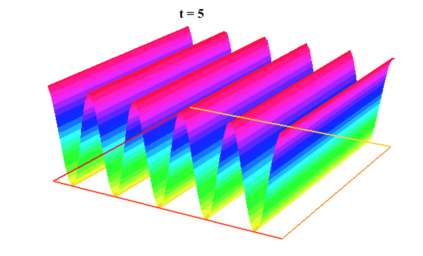
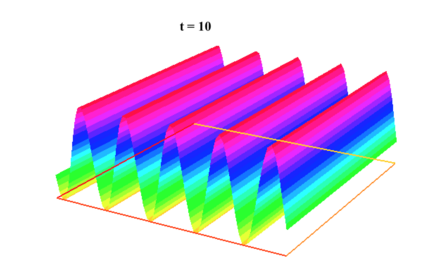
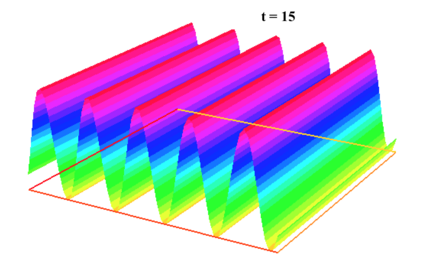
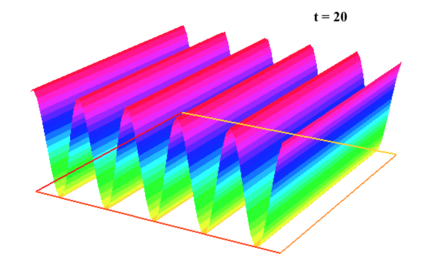
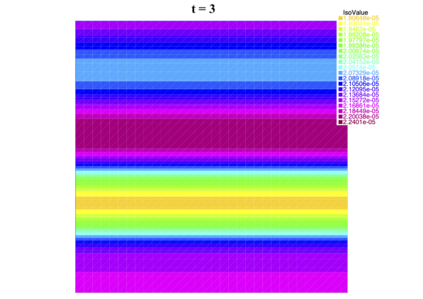
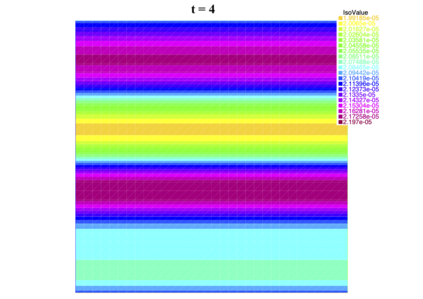
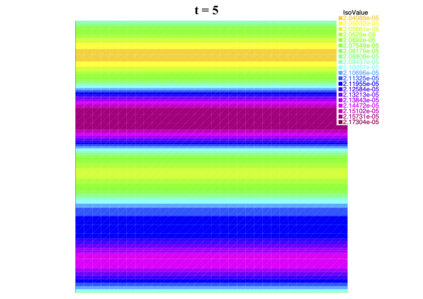
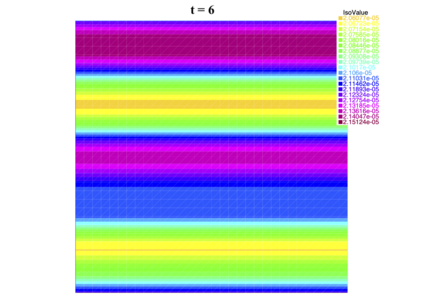
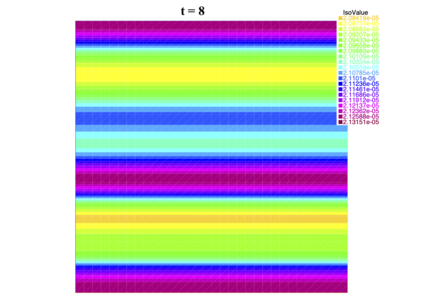
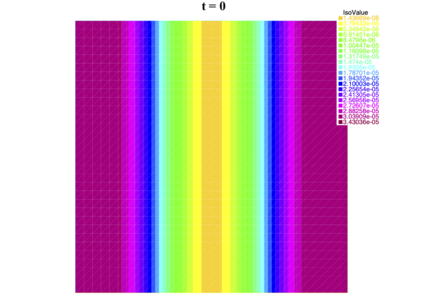
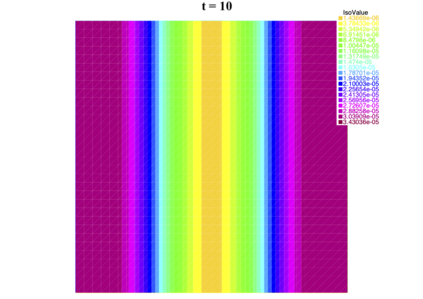
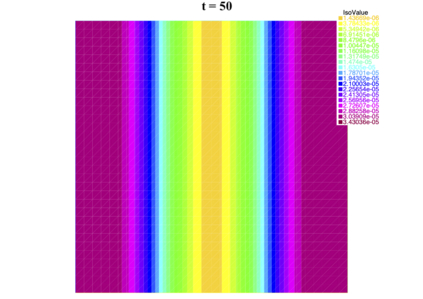
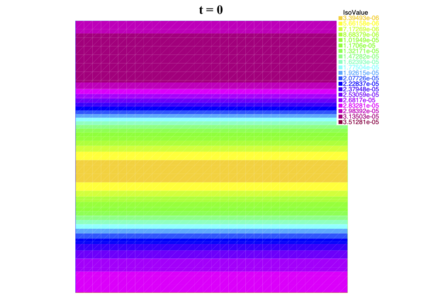
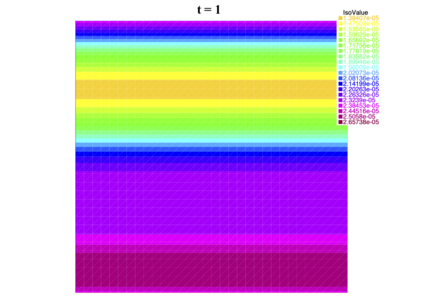
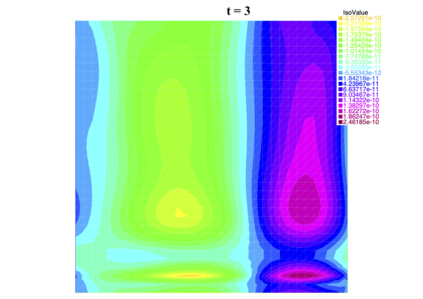
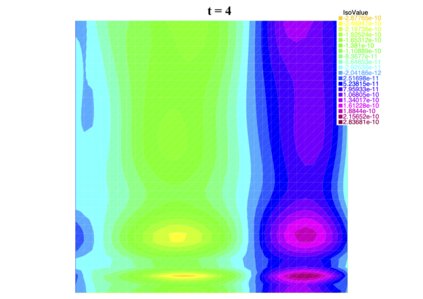
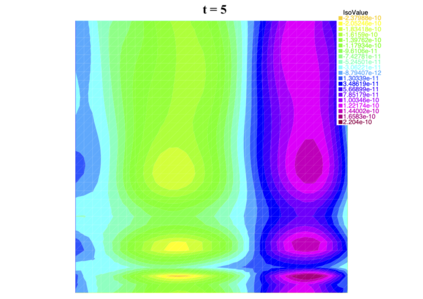
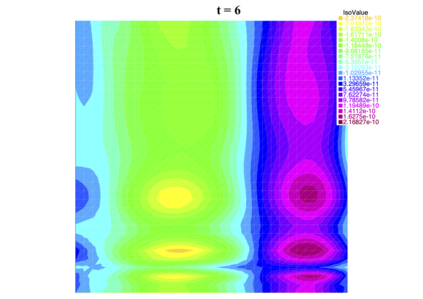
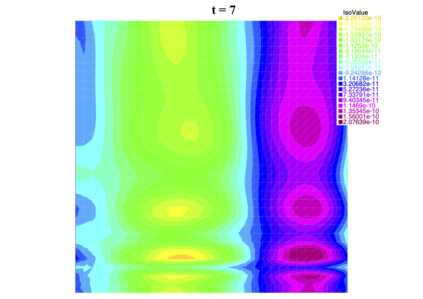
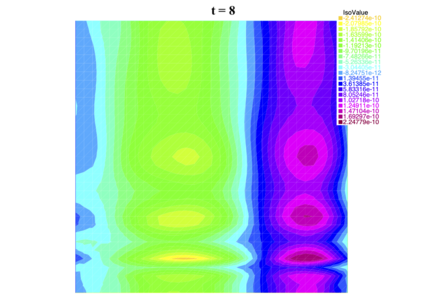
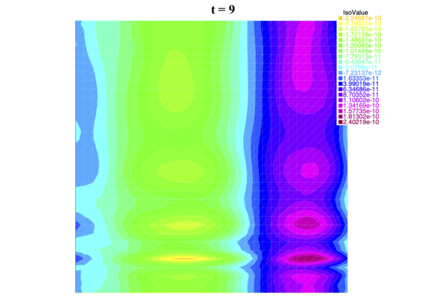
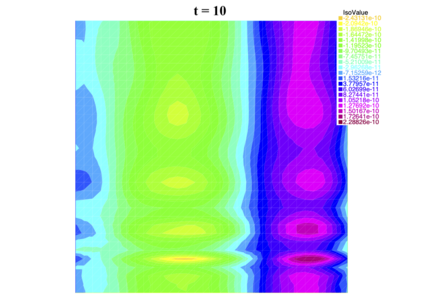
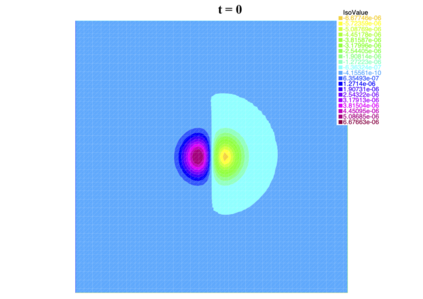
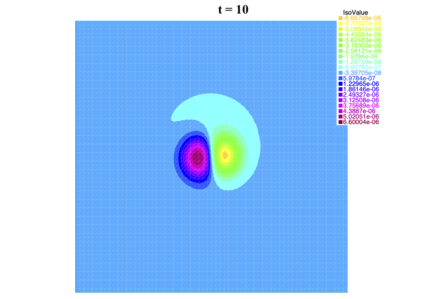
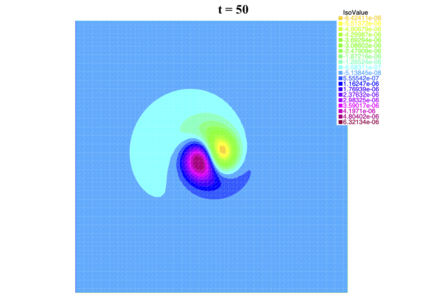
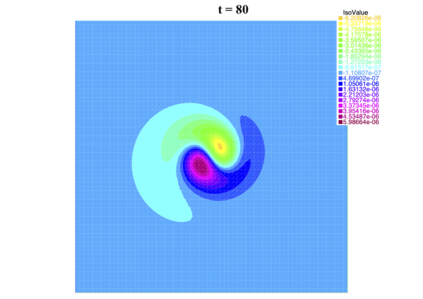
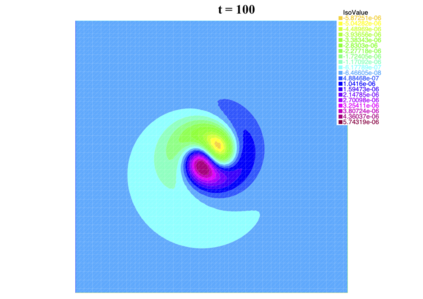
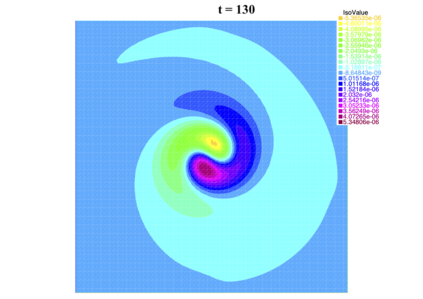
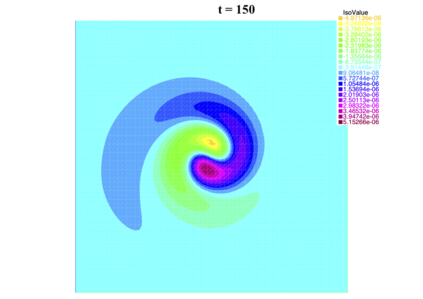
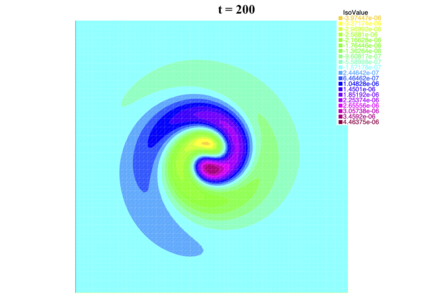
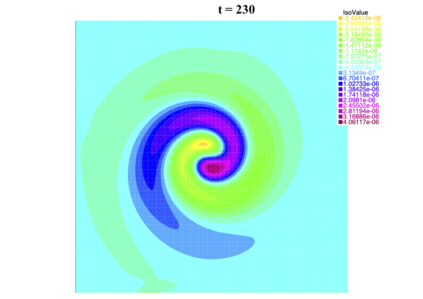
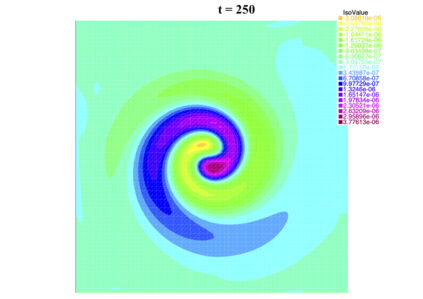
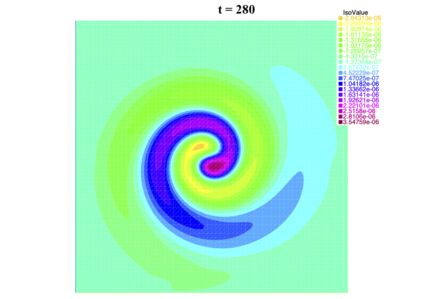
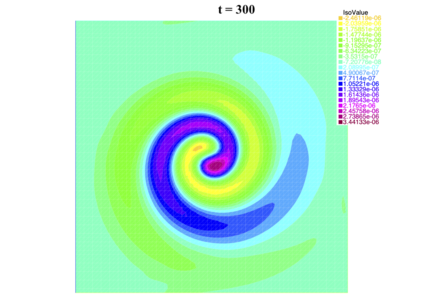
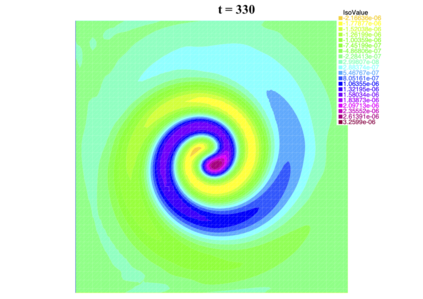
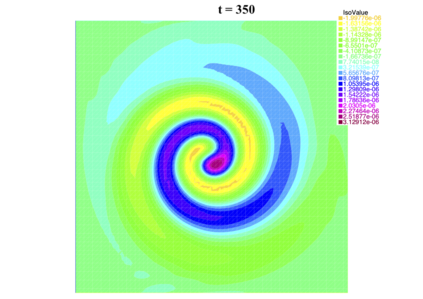
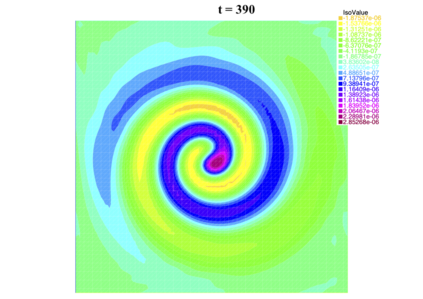
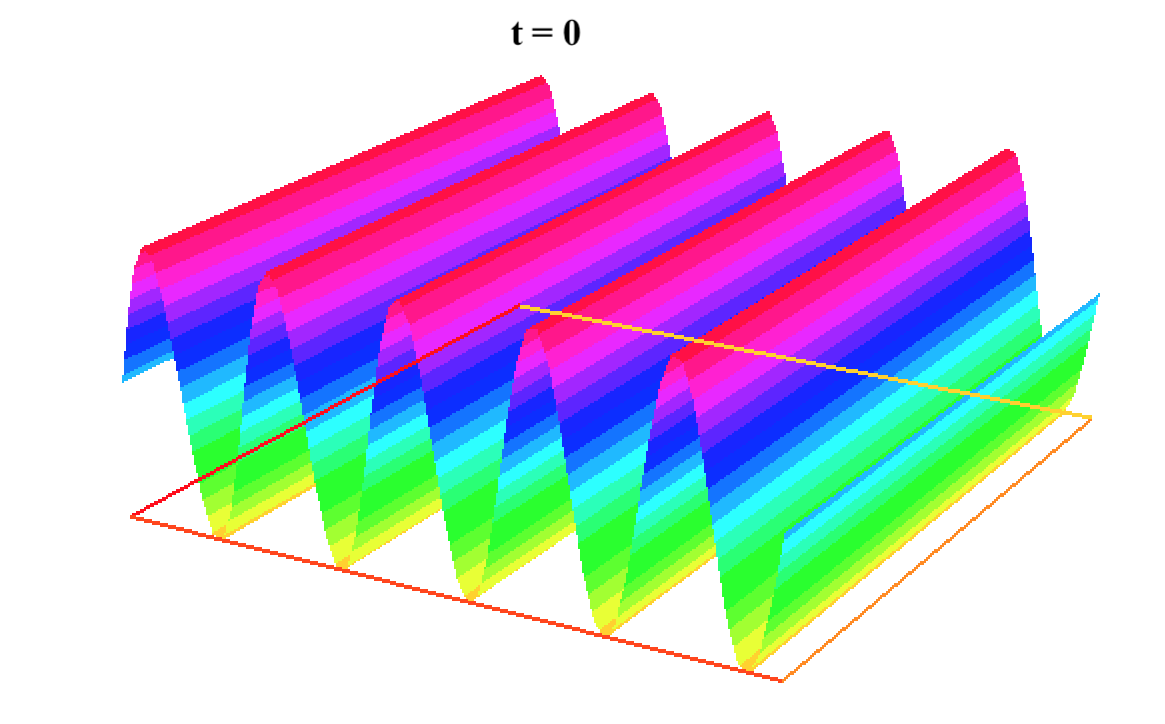
In [1], the non-linear space-time Hasegawa-Mima plasma equation is formulated as a coupled system of two linear PDE's, a solution of which is a pair (u, w). The first equation is of hyperbolic type and the second of elliptic type. Variational frames for obtaining weak solutions to the initial value Hasegawa-Mima problem with periodic boundary conditions were also derived. In a more recent work [2], a numerical approach consisting of a finite element space-domain combined with an Euler-implicit time scheme was used to discretize the coupled variational Hasegawa-Mima model. A semi-linear version of this implicit nonlinear scheme was tested for several types of initial conditions. This semi-linear scheme proved to lack efficiency for long time, which necessitates imposing a cap on the magnitude of the solution. To circumvent this difficulty, in this paper, we use Newton-type methods (Newton, Chord and an introduced Modified Newton method) to solve numerically the fully-implicit non-linear scheme. Testing these methods in FreeFEM++ indicates significant improvements as no cap needs to be imposed for long time. In the sequel, we demonstrate the validity of these methods by proving several results, in particular the convergence of the implemented methods.
翻译:[1]中,非线性空间时间长谷川-米马等离子方程式是两个线性PDE的组合系统,其解决方案是一对(u, w)。第一个等式是双曲型,第二个是椭圆型。还得出了对长谷川-米马的初始值有周期边界条件的问题获得薄弱解决方案的变式框架。在较近的一项工作[2]中,采用了由有限元素空间-域与Euler-ima不透明时间制组成的数字方法,将同时的变异长谷川-米马模型分开。对这一隐含的非线性方案的半线性版本对几种初始条件进行了测试。这一半线性办法证明长期缺乏效率,这就需要对解决办法的规模施加一个上限。为了避免这一困难,我们使用牛顿型方法(Newton,Cord,Choord和引入的Modificed Newton方法)从数字上解决完全不精确的非线性模式。在FreeEM++中测试了这些方法的半线性版本,表明这些方法的长期有效性是用来证明我们所执行的。