Solving the Dirichlet problem for the Monge-Ampère equation using neural networks

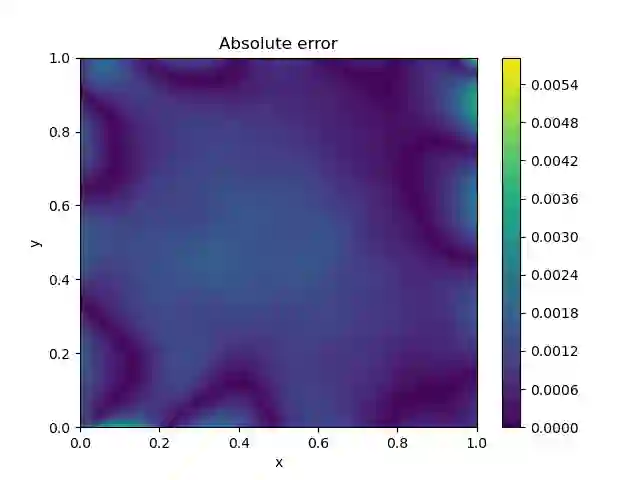
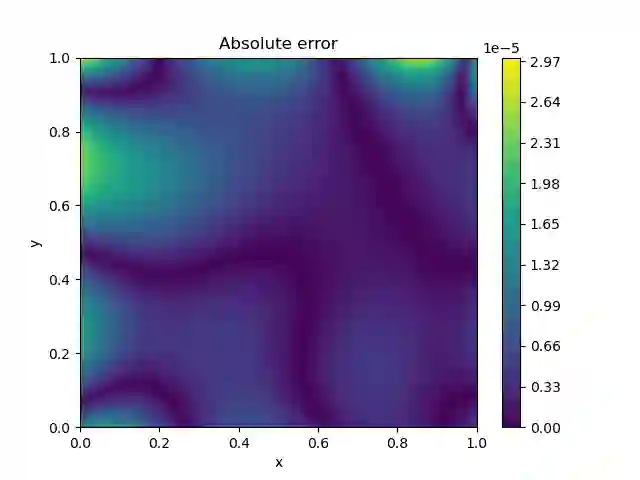
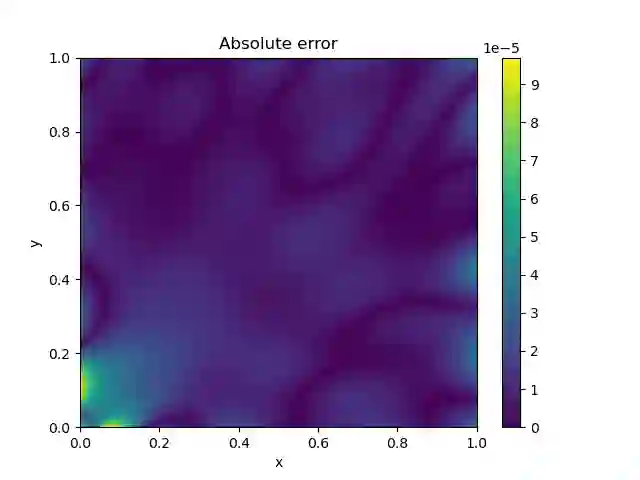
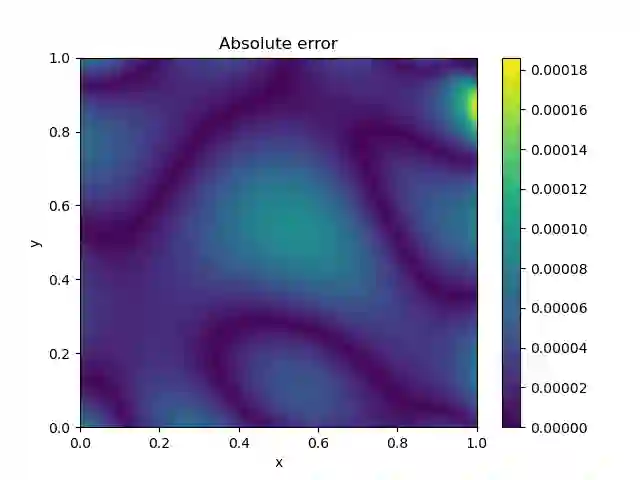
The Monge-Amp\`ere equation is a fully nonlinear partial differential equation (PDE) of fundamental importance in analysis, geometry and in the applied sciences. In this paper we solve the Dirichlet problem associated with the Monge-Amp\`ere equation using neural networks and we show that an ansatz using deep input convex neural networks can be used to find the unique convex solution. As part of our analysis we study the effect of singularities, discontinuities and noise in the source function, we consider nontrivial domains, and we investigate how the method performs in higher dimensions. We also compare this method to an alternative approach in which standard feed-forward networks are used together with a loss function which penalizes lack of convexity.