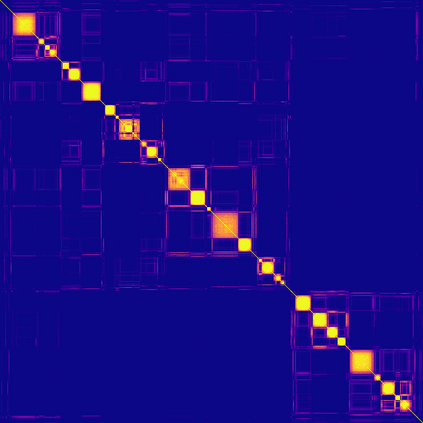
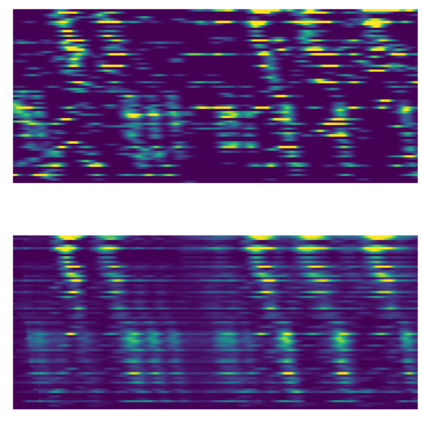
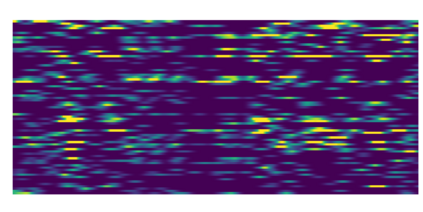
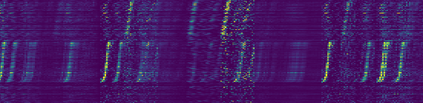
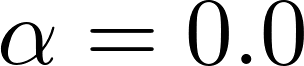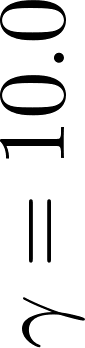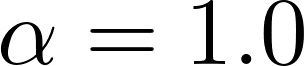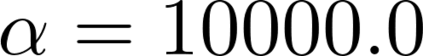Neyman-Scott processes (NSPs) are point process models that generate clusters of points in time or space. They are natural models for a wide range of phenomena, ranging from neural spike trains to document streams. The clustering property is achieved via a doubly stochastic formulation: first, a set of latent events is drawn from a Poisson process; then, each latent event generates a set of observed data points according to another Poisson process. This construction is similar to Bayesian nonparametric mixture models like the Dirichlet process mixture model (DPMM) in that the number of latent events (i.e. clusters) is a random variable, but the point process formulation makes the NSP especially well suited to modeling spatiotemporal data. While many specialized algorithms have been developed for DPMMs, comparatively fewer works have focused on inference in NSPs. Here, we present novel connections between NSPs and DPMMs, with the key link being a third class of Bayesian mixture models called mixture of finite mixture models (MFMMs). Leveraging this connection, we adapt the standard collapsed Gibbs sampling algorithm for DPMMs to enable scalable Bayesian inference on NSP models. We demonstrate the potential of Neyman-Scott processes on a variety of applications including sequence detection in neural spike trains and event detection in document streams.
翻译:内曼- 斯科特进程( Neyman- Scott process (NSPs) 是产生时间或空间点群集的点点进程模型。 它们是一系列现象的自然模型, 从神经钉钉列列列到文档流。 组合属性是通过双重的随机配置实现的: 首先, 一组潜在事件是从 Poisson 进程绘制的; 然后, 每个潜在事件都根据另一个 Poisson 进程生成一套观察到的数据点。 这种构造类似于巴伊西亚非参数混合模型( Drichlet 混合模型)等非参数混合模型, 其潜在事件( e. groups) 是一个随机变量, 但点进程设计使NSP 特别适合模拟随机数据 。 虽然为DPMMs 开发了许多专门的算法, 但相对较少的工程侧重于NSP 的推断。 这里, 我们展示了NDPMS 和DPMS 标准崩溃检测序列程序之间的新型链接, 其关键链接是被称为Bayesman mindent mix mind 模型 (MMs ) 。 。 在连接中, 我们从这个链接中演示了NCalembal 中演示了NMSP 标准的崩溃检测序列序列序列序列,,,, 以显示了NMMS 使 Bay mactal- sablecolvecal sable imcol