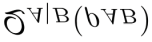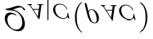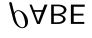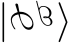Large-scale quantum networks have been employed to overcome practical constraints of transmissions and storage for single entangled systems. Our goal in this article is to explore the strong entanglement distribution of quantum networks. We firstly show any connected network consisting of generalized EPR states and GHZ states satisfies strong CKW monogamy inequality in terms of bipartite entanglement measure. This reveals interesting feature of high-dimensional entanglement with local tensor decomposition going beyond qubit entanglement. We then apply the new entanglement distribution relation in entangled networks for getting quantum max-flow min-cut theorem in terms of von Neumann entropy and R\'{e}nyi-$\alpha$ entropy. We finally classify entangled quantum networks by distinguishing network configurations under local unitary operations. These results provide new insights into characterizing quantum networks in quantum information processing.
翻译:大型量子网络已被用于克服传输和存储单一缠绕系统的实际限制。 我们的这一条的目标是探索量子网络的强烈缠绕分布。 我们首先展示由普遍 EPR 状态和 GHZ 状态组成的任何连接网络, 在双面缠绕测量中, 满足了强大的 CKW 一等不平等。 这揭示了高维纠缠与本地多压分解的有趣特征, 超越了Qubit 缠绕。 我们随后在缠绕的网络中应用新的纠缠分布关系, 以获得 von Neuumann entropy 和 R\\\ {e} nyi- $\ alpha$ entropy 的量子流微剪线。 我们最后通过区分本地统一操作下的网络配置, 最终对缠绕的量子网络进行了分类。 这些结果为量子信息处理中的量子网络定性提供了新的洞察。