Neural Koopman Lyapunov Control

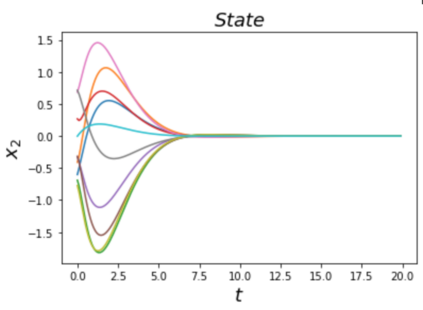
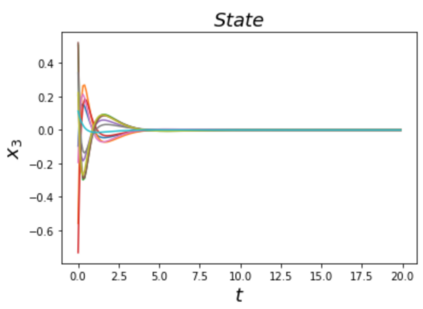
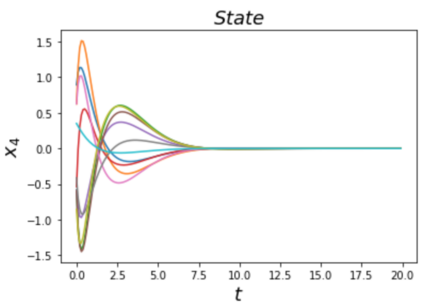
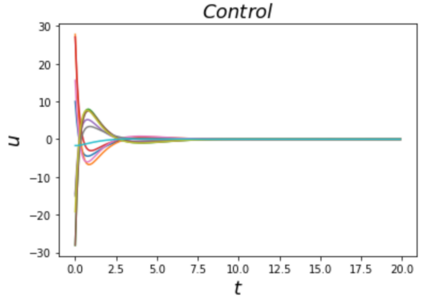
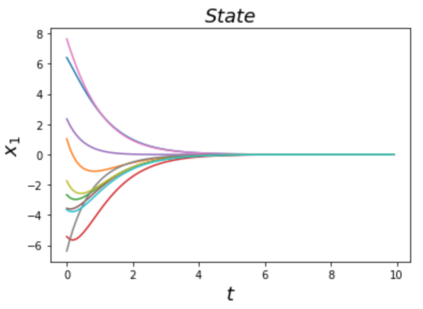
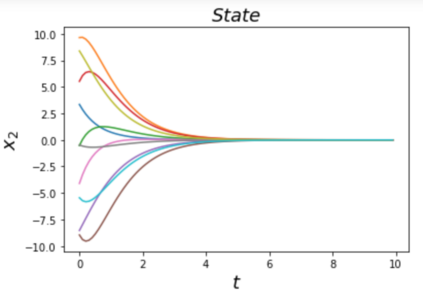
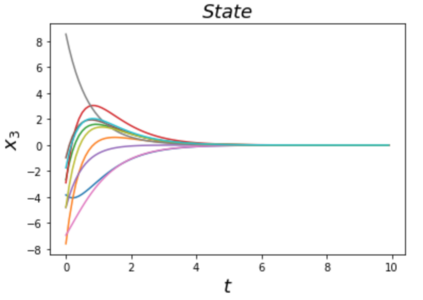
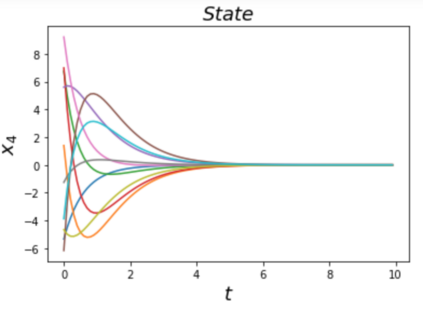
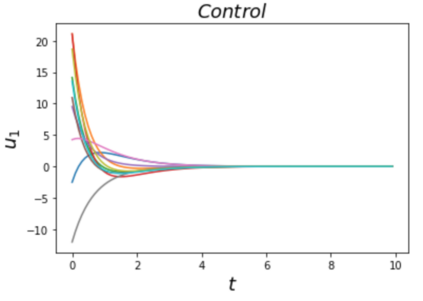
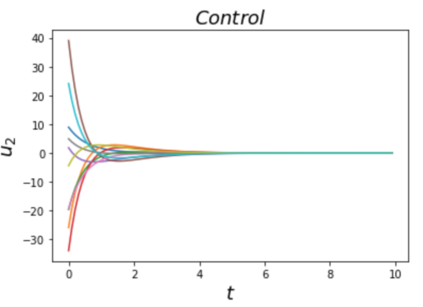
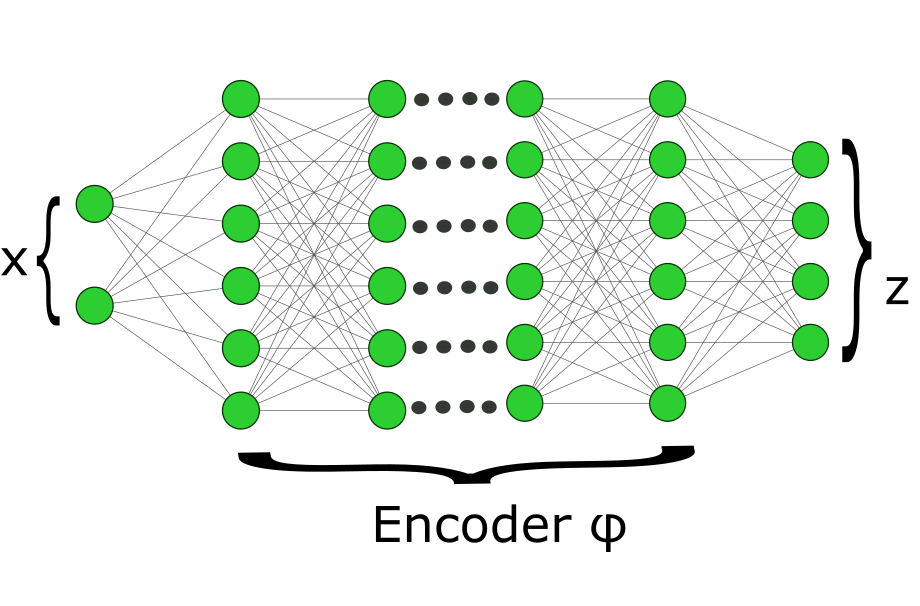
Learning and synthesizing stabilizing controllers for unknown nonlinear systems is a challenging problem for real-world and industrial applications. Koopman operator theory allow one to analyze nonlinear systems through the lens of linear systems and nonlinear control systems through the lens of bilinear control systems. The key idea of these methods, lies in the transformation of the coordinates of the nonlinear system into the Koopman observables, which are coordinates that allow the representation of the original system (control system) as a higher dimensional linear (bilinear control) system. However, for nonlinear control systems, the bilinear control model obtained by applying Koopman operator based learning methods is not necessarily stabilizable and therefore, the existence of a stabilizing feedback control is not guaranteed which is crucial for many real world applications. Simultaneous identification of these stabilizable Koopman based bilinear control systems as well as the associated Koopman observables is still an open problem. In this paper, we propose a framework to identify and construct these stabilizable bilinear models and its associated observables from data by simultaneously learning a bilinear Koopman embedding for the underlying unknown nonlinear control system as well as a Control Lyapunov Function (CLF) for the Koopman based bilinear model using a learner and falsifier. Our proposed approach thereby provides provable guarantees of global asymptotic stability for the nonlinear control systems with unknown dynamics. Numerical simulations are provided to validate the efficacy of our proposed class of stabilizing feedback controllers for unknown nonlinear systems.