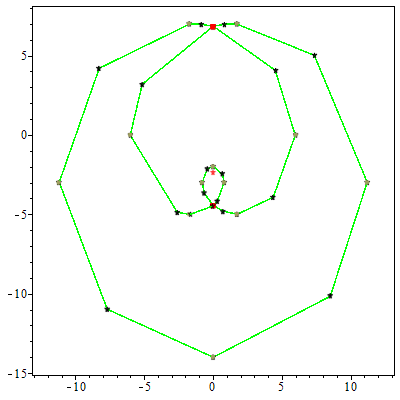
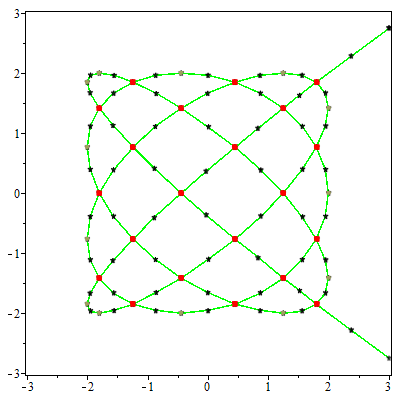
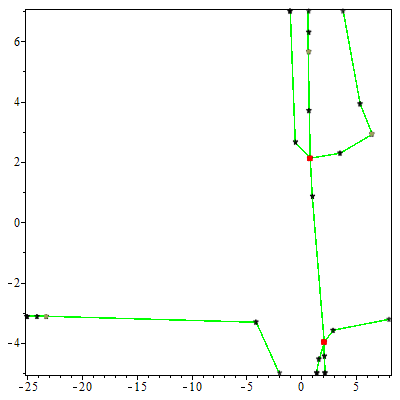
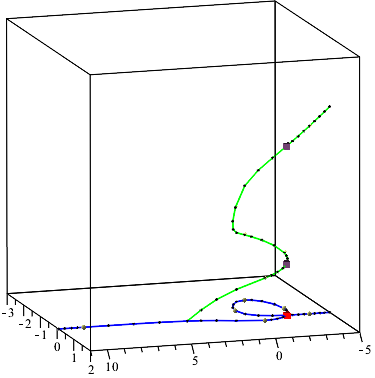
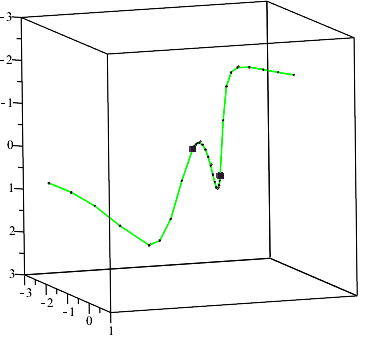
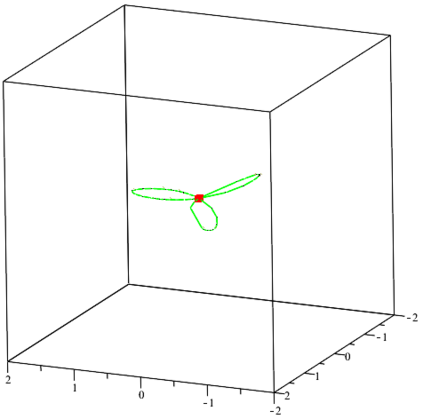
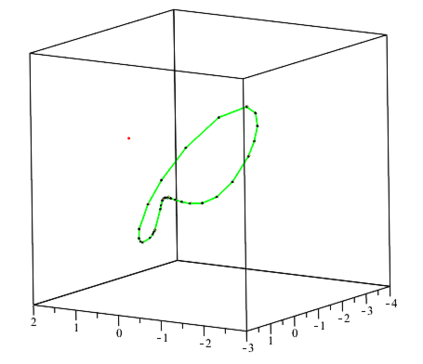
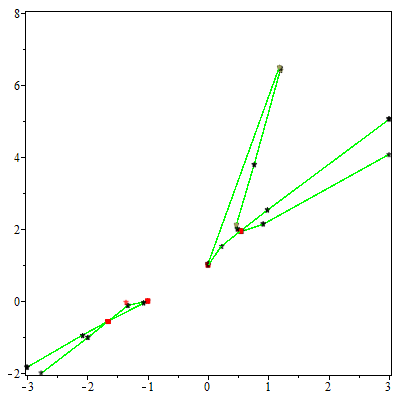
We consider the problem of computing the topology and describing the geometry of a parametric curve in $\mathbb{R}^n$. We present an algorithm, PTOPO, that constructs an abstract graph that is isotopic to the curve in the embedding space. Our method exploits the benefits of the parametric representation and does not resort to implicitization. Most importantly, we perform all computations in the parameter space and not in the implicit space. When the parametrization involves polynomials of degree at most $d$ and maximum bitsize of coefficients $\tau$, then the worst case bit complexity of PTOPO is $ \tilde{\mathcal{O}}_B(nd^6+nd^5\tau+d^4(n^2+n\tau)+d^3(n^2\tau+ n^3)+n^3d^2\tau)$. This bound matches the current record bound $\tilde{\mathcal{O}}_B(d^6+d^5\tau)$ for the problem of computing the topology of a plane algebraic curve given in implicit form. For plane and space curves, if $N = \max\{d, \tau \}$, the complexity of PTOPO becomes $\tilde{\mathcal{O}}_B(N^6)$, which improves the state-of-the-art result, due to Alc\'azar and D\'iaz-Toca [CAGD'10], by a factor of $N^{10}$. In the same time complexity, we obtain a graph whose straight-line embedding is isotopic to the curve. However, visualizing the curve on top of the abstract graph construction, increases the bound to $\tilde{\mathcal{O}}_B(N^7)$. For curves of general dimension, we can also distinguish between ordinary and non-ordinary real singularities and determine their multiplicities in the same expected complexity of PTOPO by employing the algorithm of Blasco and P\'erez-D\'iaz [CAGD'19]. We have implemented PTOPO in Maple for the case of plane and space curves. Our experiments illustrate its practical nature.
翻译:我们考虑的是计算表层和描述以$mathb{R%n$计算的参数曲线的几何问题。 我们展示了一个算法, PTOPO, 这个算法是一个与嵌入空间的曲线相对的抽象图。 我们的方法利用了参数表达法的好处, 而不是隐含化。 最重要的是, 我们在参数空间而不是隐含空间中进行所有计算。 当参数化涉及到最多以$和最大比值的多位化程度。 当当前记录以$和最大比值的位数计算时, 那么, PTOPO 最差的情况是 $\ telde_cal =ocal。 P6+_nd_5\ tã+d%4(n2+n_tau) +d%3, 而不是在隐性空间中进行计算。 当目前记录以$d_d_tal_tal_tal_tal_caal_tal_tal_tal_tal_tal_tal_tal_tal_tal_ ligral_toal_ mamama_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ dal_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_d_d_d_d_d_d_d_d_d_d_d_d_d_d_d_d_d_d_d_d_d_d_d_d_d_d_d_d_d_d_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_d_ ma_ ma_d_d_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_ ma_