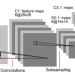
Convolutional neural network image classifiers are defined and the rate of convergence of the misclassification risk of the estimates towards the optimal misclassification risk is analyzed. Here we consider images as random variables with values in some functional space, where we only observe discrete samples as function values on some finite grid. Under suitable structural and smoothness assumptions on the functional a posteriori probability, which includes some kind of symmetry against rotation of subparts of the input image, it is shown that least squares plug-in classifiers based on convolutional neural networks are able to circumvent the curse of dimensionality in binary image classification if we neglect a resolution-dependent error term. The finite sample size behavior of the classifier is analyzed by applying it to simulated and real data.
翻译:定义了进化神经网络图像分类,并分析了估算误分类风险与最佳误分类风险的趋同率。 在这里, 我们将图像视为随机变量, 在某些功能空间里, 我们只观察离散样本作为某些有限网格的函数值。 根据对功能后生概率的适当的结构性和平稳假设, 包括对输入图像子部分的旋转进行某种对称, 显示基于进化神经网络的最小方形插件分类器, 如果我们忽略一个基于分辨率的错误术语, 就可以绕过二元图像分类中的维度诅咒。 将分类器的有限样本大小行为应用到模拟和真实数据中进行分析 。