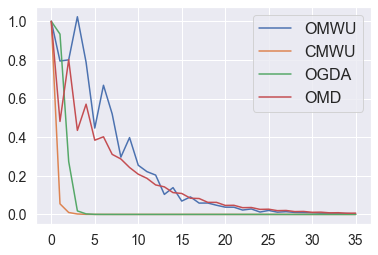
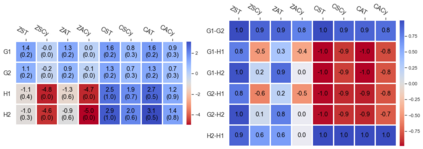
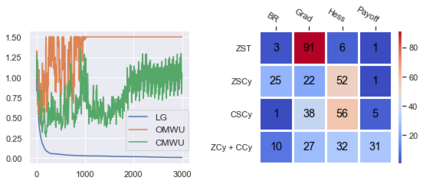
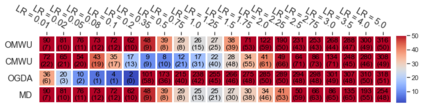
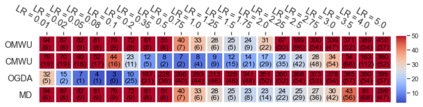
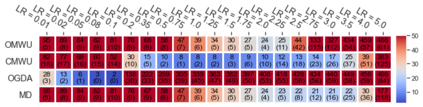
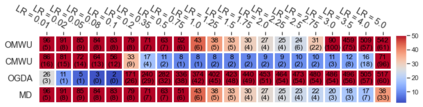
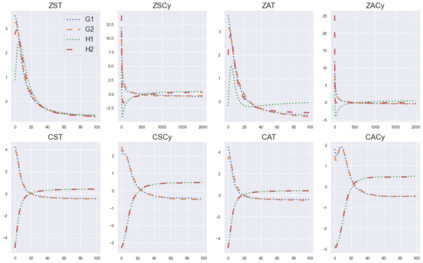
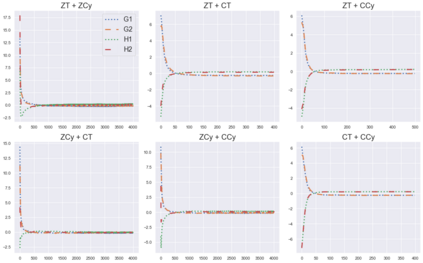
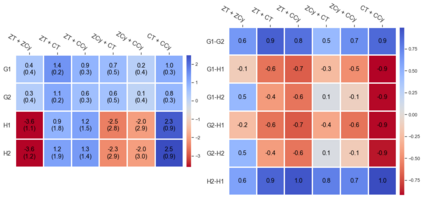
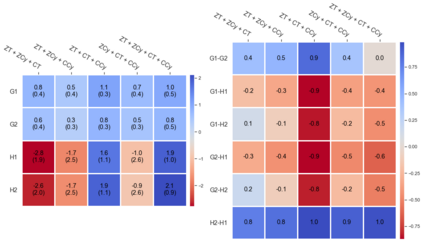
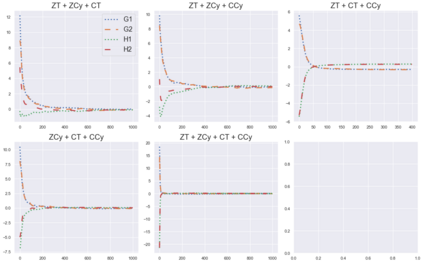
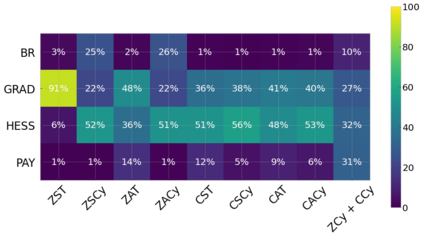
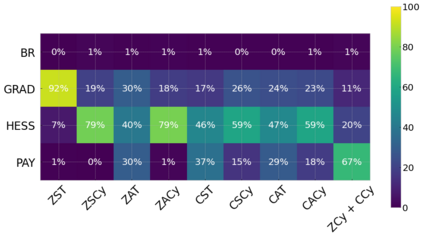
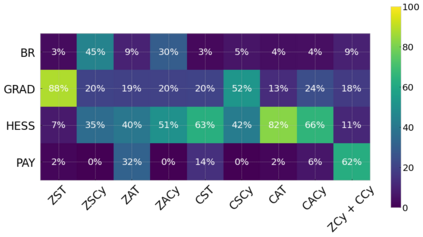
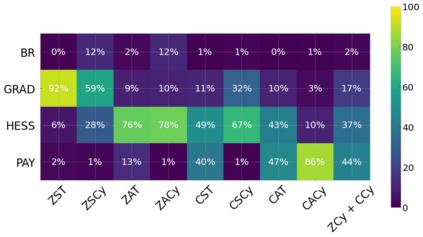
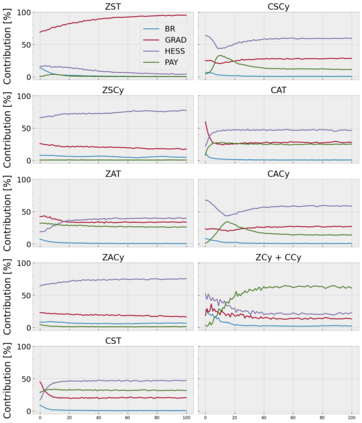
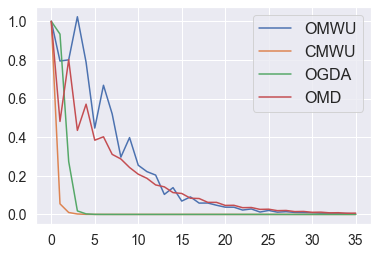
Cheung and Piliouras (2020) recently showed that two variants of the Multiplicative Weights Update method - OMWU and MWU - display opposite convergence properties depending on whether the game is zero-sum or cooperative. Inspired by this work and the recent literature on learning to optimize for single functions, we introduce a new framework for learning last-iterate convergence to Nash Equilibria in games, where the update rule's coefficients (learning rates) along a trajectory are learnt by a reinforcement learning policy that is conditioned on the nature of the game: \textit{the game signature}. We construct the latter using a new decomposition of two-player games into eight components corresponding to commutative projection operators, generalizing and unifying recent game concepts studied in the literature. We compare the performance of various update rules when their coefficients are learnt, and show that the RL policy is able to exploit the game signature across a wide range of game types. In doing so, we introduce CMWU, a new algorithm that extends consensus optimization to the constrained case, has local convergence guarantees for zero-sum bimatrix games, and show that it enjoys competitive performance on both zero-sum games with constant coefficients and across a spectrum of games when its coefficients are learnt.
翻译:张光朗(2020年)和张光朗(2020年)最近显示,根据游戏的零和或合作性,多倍 Weights更新方法的两个变体----OMWU和MWU----显示了两个不同的趋同特性,这取决于游戏是零和还是合作性。受这项工作和最近关于学习优化单一功能的文献的启发,我们引入了一个新的框架,学习游戏中Nash Equiliburia的最后一流趋同,在游戏中学习了更新规则的系数(学习率),沿轨迹学习了一种以游戏性质为条件的强化学习政策:\ textit{the game 签名}。我们用两个玩家游戏的新的分解组合组成八个组成部分来构建后者。我们比较了各种更新规则在学习系数时的表现,并表明RL政策能够将游戏的签名用于广泛的游戏类型。我们这样做时,我们引入了一种新的算法,即将共识优化扩展到受限制的情况,对零和双基游戏的组合游戏具有本地的保证,并且显示它具有竞争力的系数。