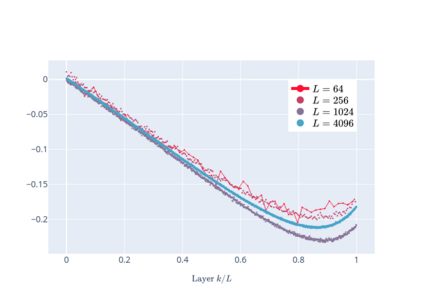
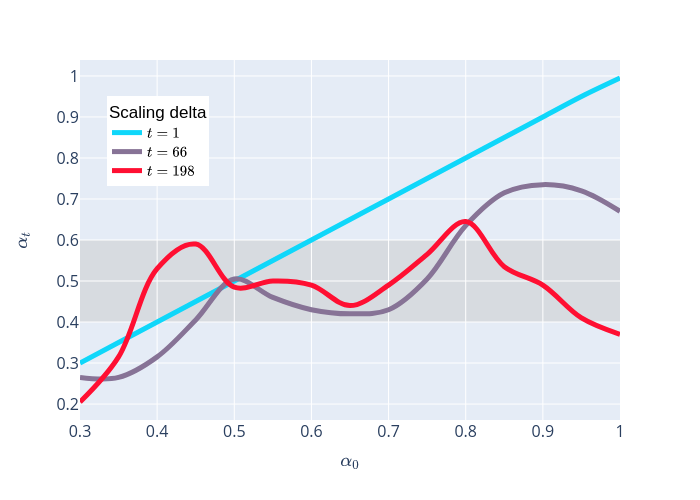
We prove linear convergence of gradient descent to a global optimum for the training of deep residual networks with constant layer width and smooth activation function. We show that if the trained weights, as a function of the layer index, admit a scaling limit as the depth increases, then the limit has finite $p-$variation with $p=2$. Proofs are based on non-asymptotic estimates for the loss function and for norms of the network weights along the gradient descent path. We illustrate the relevance of our theoretical results to practical settings using detailed numerical experiments on supervised learning problems.
翻译:我们证明,梯度下降与培训具有常态层宽度和平稳激活功能的深层残余网络的全球最佳水平呈线性趋同。我们证明,如果经过训练的重量作为层指数的函数,在深度增加时接受一个缩放限度,那么这一限度就以美元=2美元为单位的限定值。证据的依据是对梯度下降路径上的损失函数和网络重量规范的非被动估计值。我们用对监管的学习问题进行的详细数字实验来说明我们的理论结果与实际环境的相关性。