Core-Elements for Classical Linear Regression

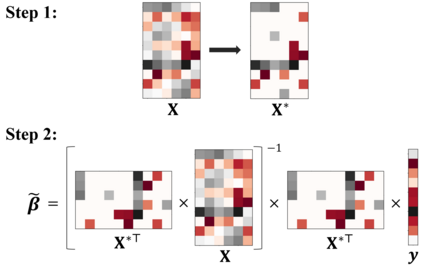
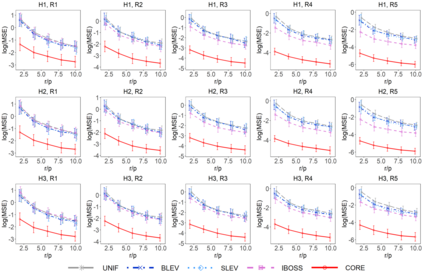
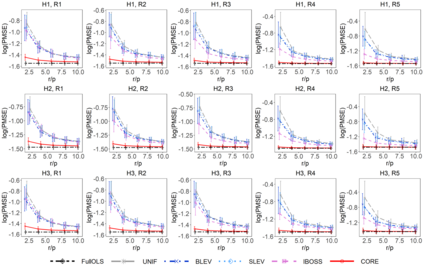
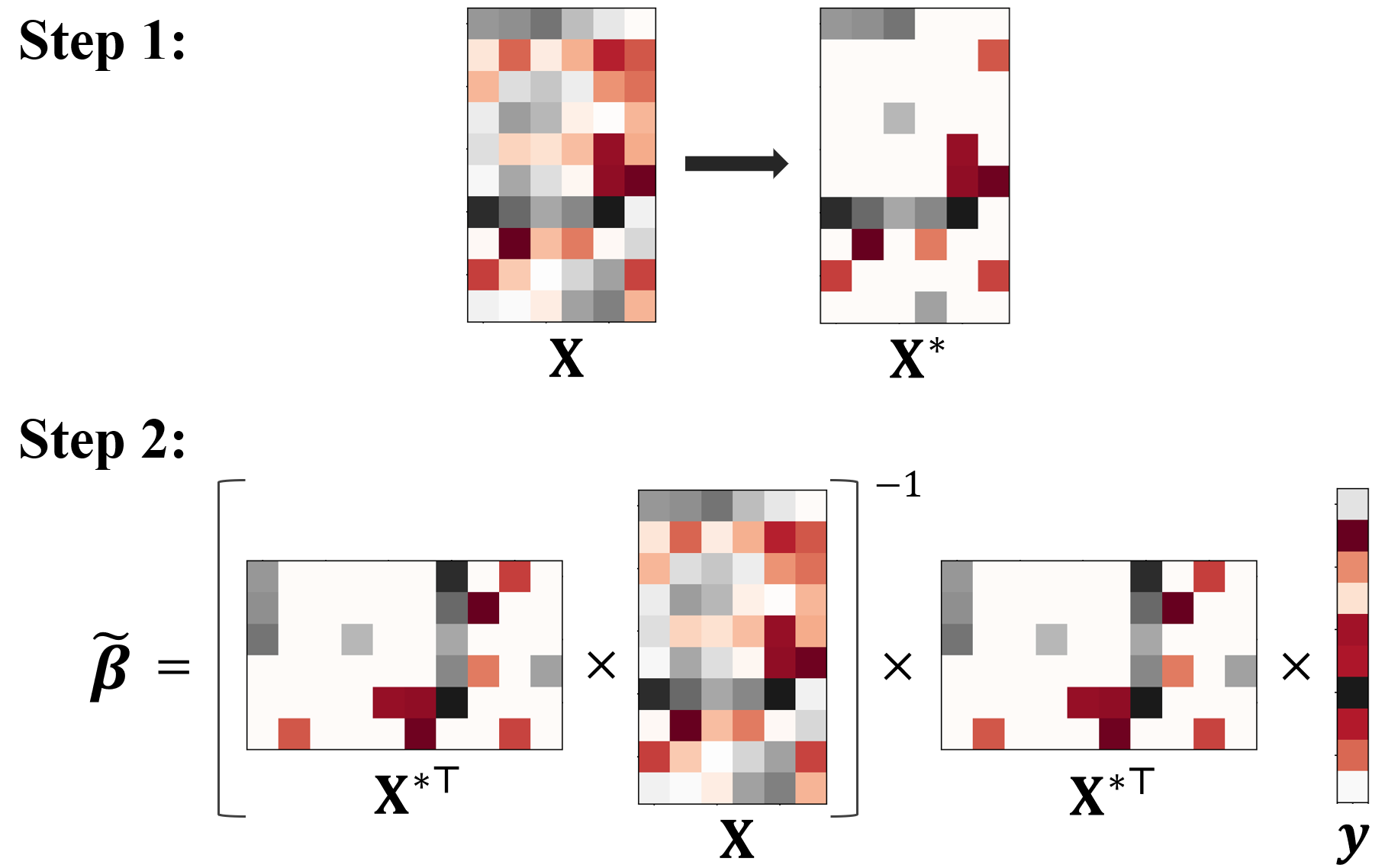
The coresets approach, also called subsampling or subset selection, aims to select a subsample as a surrogate for the observed sample. Such an approach has been used pervasively in large-scale data analysis. Existing coresets methods construct the subsample using a subset of rows from the predictor matrix. Such methods can be significantly inefficient when the predictor matrix is sparse or numerically sparse. To overcome the limitation, we develop a novel element-wise subset selection approach, called core-elements, for large-scale least squares estimation in classical linear regression. We provide a deterministic algorithm to construct the core-elements estimator, only requiring an $O(\mbox{nnz}(\mathbf{X})+rp^2)$ computational cost, where $\mathbf{X}$ is an $n\times p$ predictor matrix, $r$ is the number of elements selected from each column of $\mathbf{X}$, and $\mbox{nnz}(\cdot)$ denotes the number of non-zero elements. Theoretically, we show that the proposed estimator is unbiased and approximately minimizes an upper bound of the estimation variance. We also provide an approximation guarantee by deriving a coresets-like finite sample bound for the proposed estimator. To handle potential outliers in the data, we further combine core-elements with the median-of-means procedure, resulting in an efficient and robust estimator with theoretical consistency guarantees. Numerical studies on various synthetic and open-source datasets demonstrate the proposed method's superior performance compared to mainstream competitors.