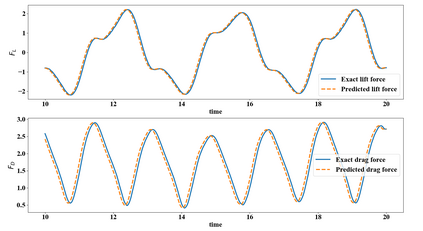
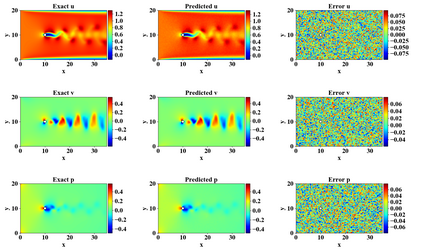
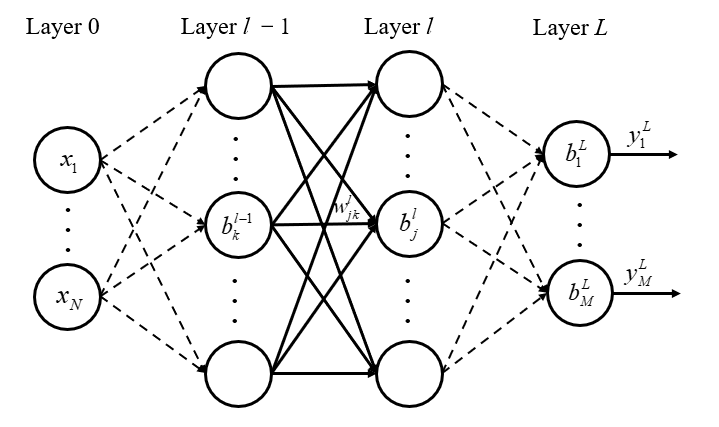
Deep learning method has attracted tremendous attention to handle fluid dynamics in recent years. However, the deep learning method requires much data to guarantee the generalization ability and the data of fluid dynamics are deficient. Recently, physics informed neural network (PINN) is popular to solve the fluid flow problems, which basic concept is to embed the governing equation and continuity equation into loss function, with the requirement of less dataset for obtaining a reliable neural network. In this paper, the mixed-variable PINN method, which convert the governing equation into continuum and constitutive formulations, is proposed to solve the fluid dynamics (flow past cylinder) without any labeled data. The initial/boundary conditions with penalty factors are also embedded into the loss function to become a well-imposed problem. The results show that mixed-variable PINN has better predictive ability to construct the flow field than traditional PINN scheme. Furthermore, the transfer learning method is adopted to is solve the fluid solutions with different Reynold numbers with less computational cost. The results also demonstrate that the transfer learning method can well simulate the different Reynolds number in a short time.
翻译:近些年来,深层学习方法吸引了处理流体动态的极大关注。然而,深层学习方法需要大量数据来保证一般化能力,而流体动态数据也不足。最近,物理知情神经网络(PINN)对于解决流体流问题很受欢迎,其基本概念是将治理方程式和连续性方程式嵌入流失功能,而对于获取可靠的神经网络则需要较少的数据集。在本文中,将治理方程式转换成连续体和构件的混合可变PINN方法被提出来在没有标签数据的情况下解决流体动态(流过气瓶)问题。带有惩罚因素的初始/封闭性条件也嵌入了损失函数中,以成为一个很好的问题。结果显示,混合可变式 PINN 系统比传统的 PINN 计划更具有更好的预测能力来构建流体字段。此外,转移学习方法是用不同的Reynold 数字和较少计算成本解决流体流体解决方案。结果还表明,转移学习方法可以在短时间内模拟不同的 Renold 数字。