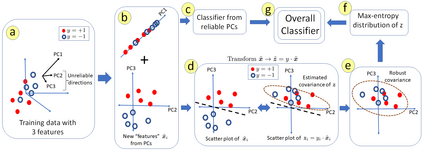
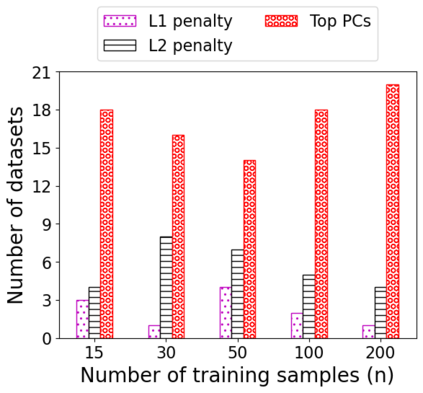
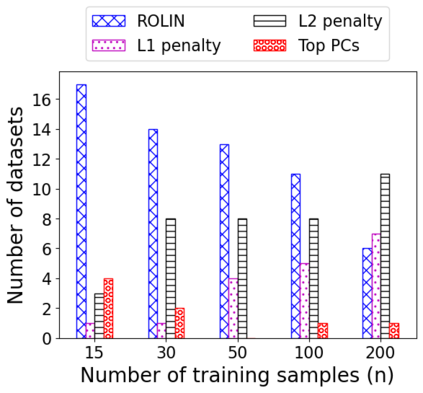
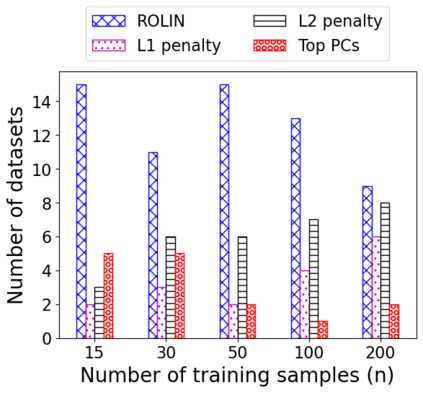
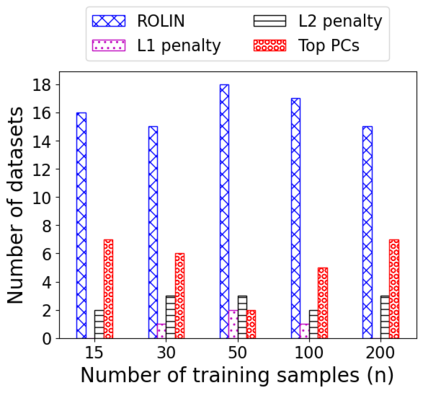
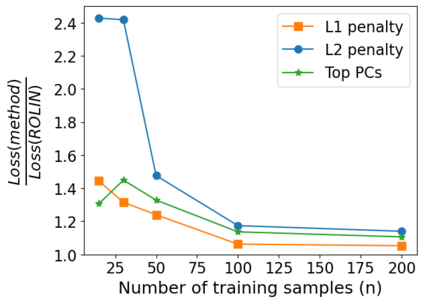
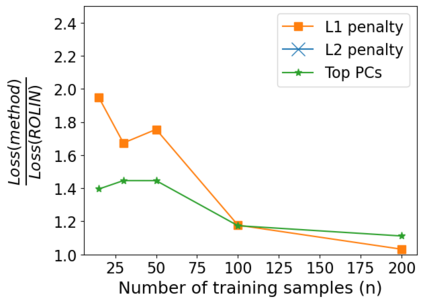
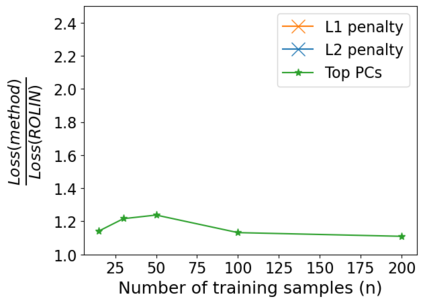
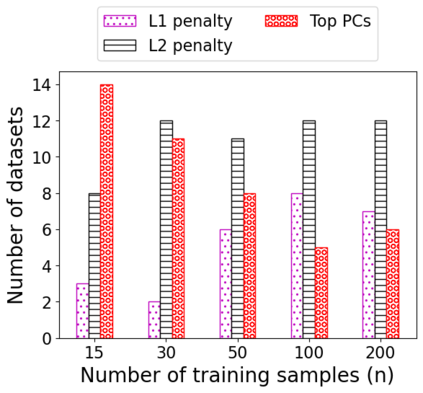
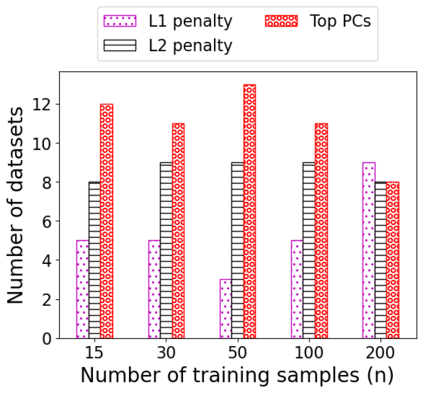
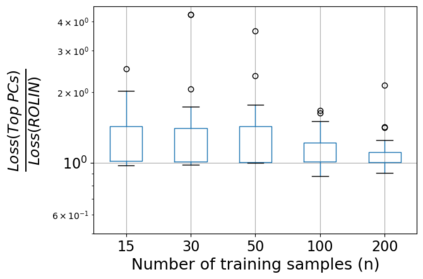
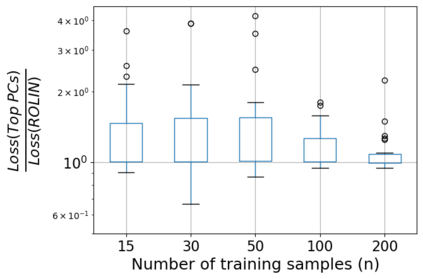
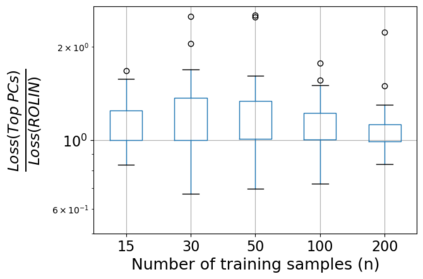
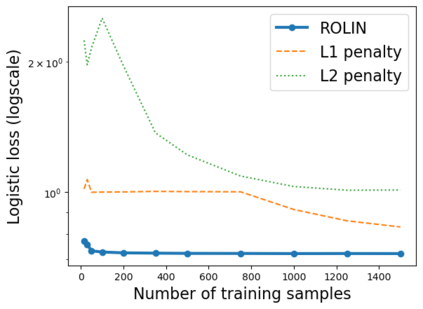
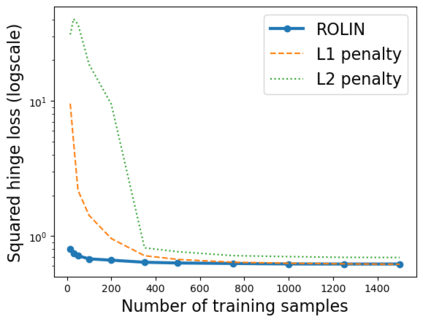
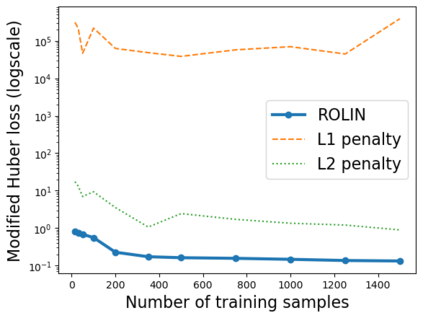
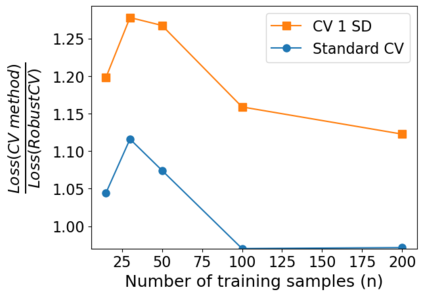
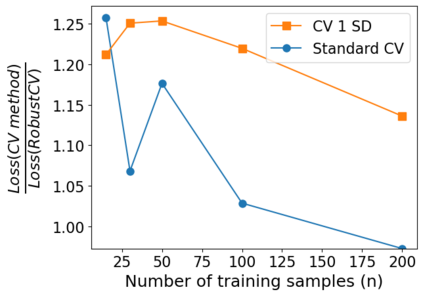
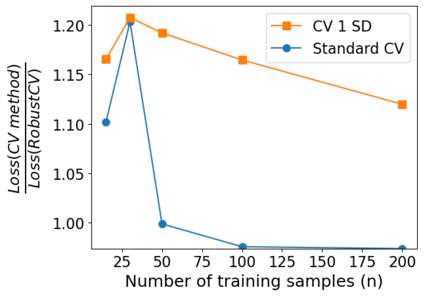
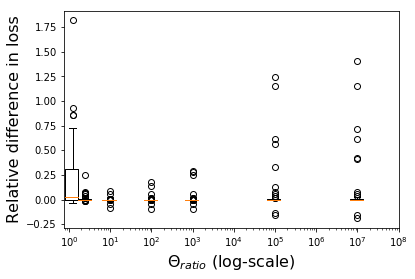
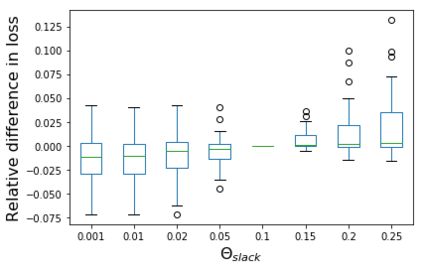
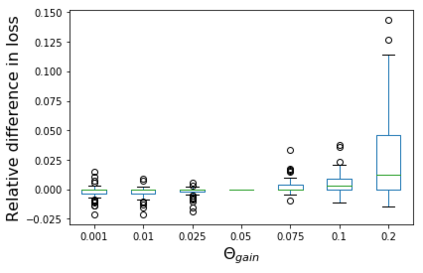
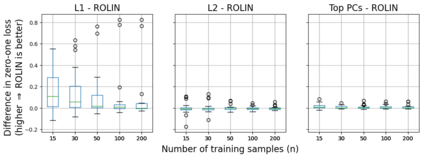
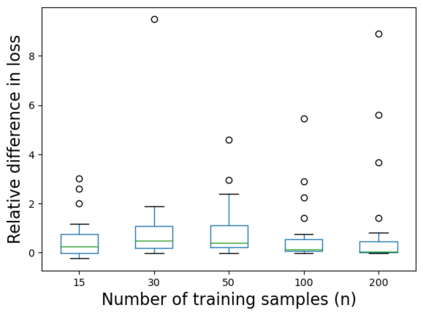
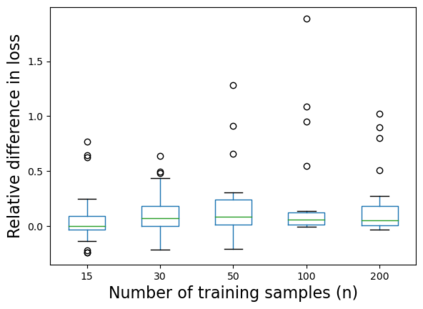
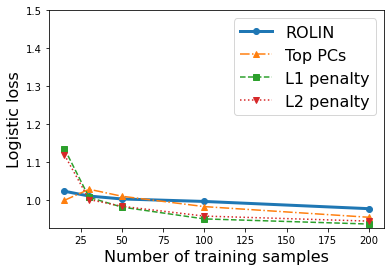
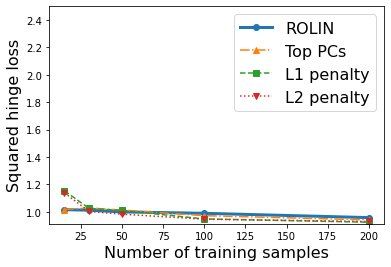
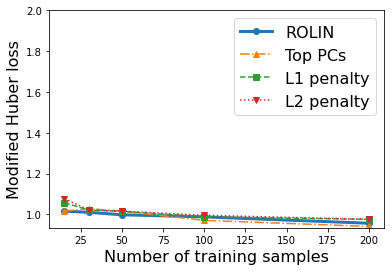
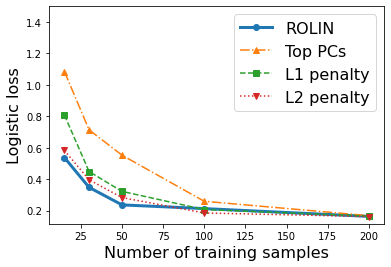
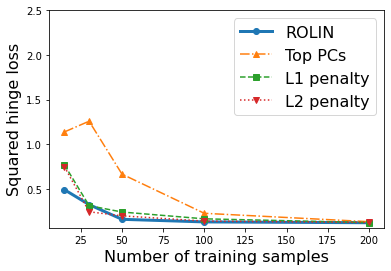
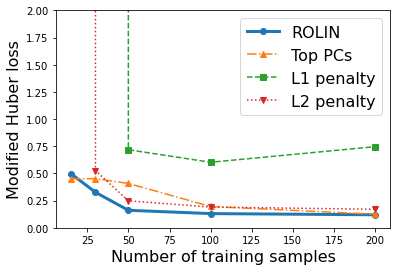
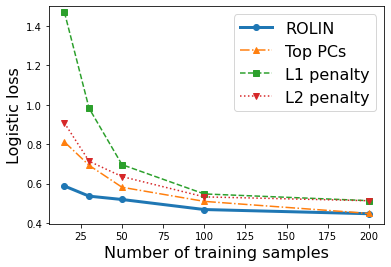
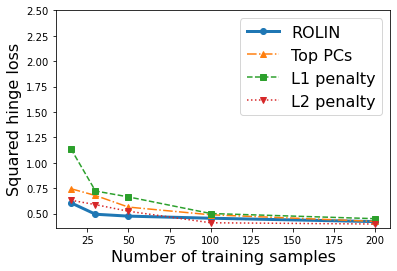
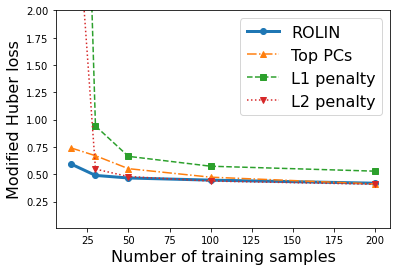
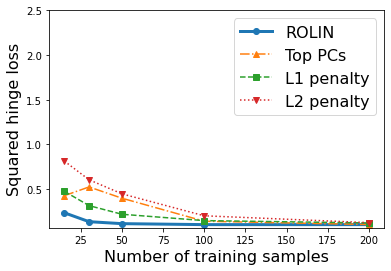
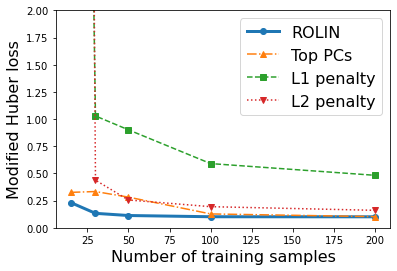
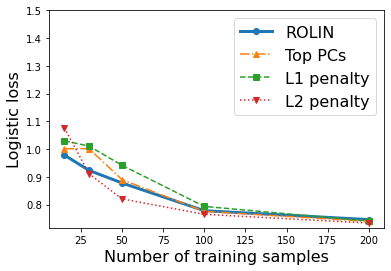
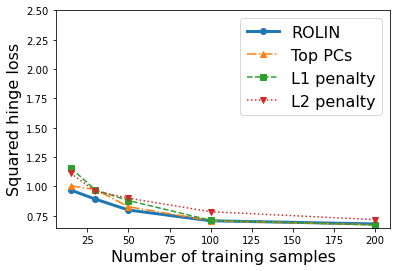
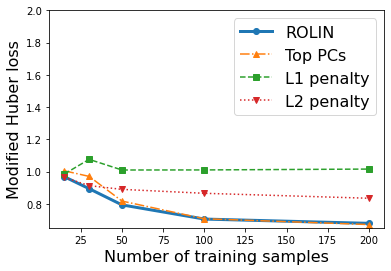
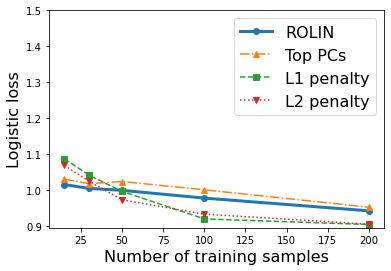
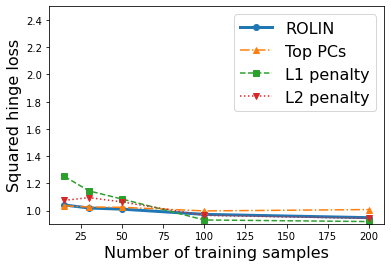
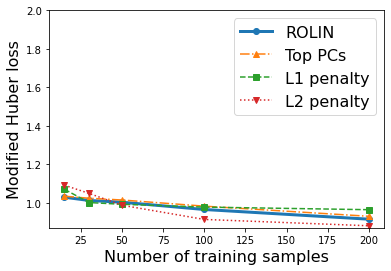
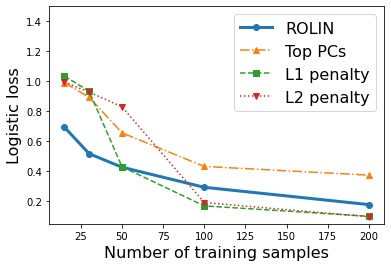
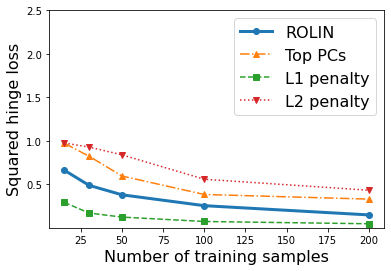
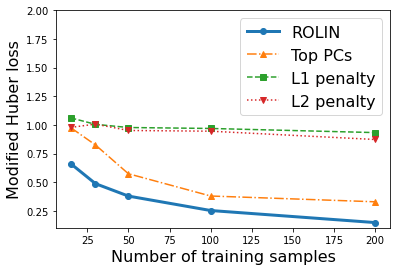
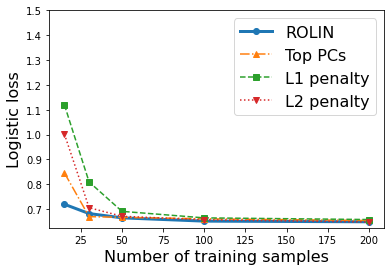
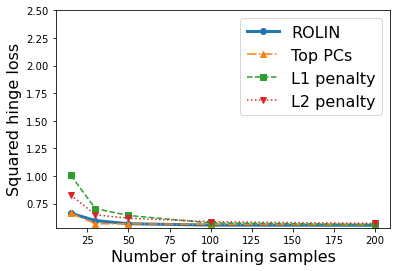
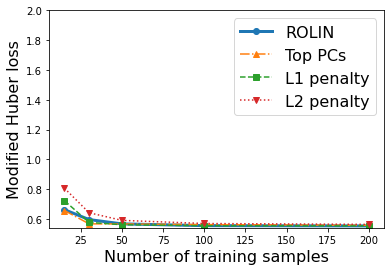
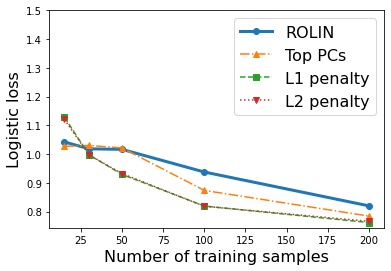
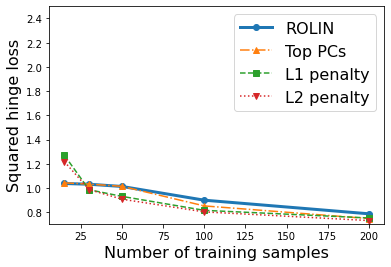
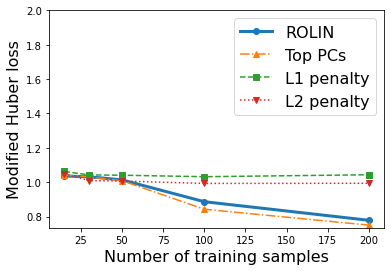
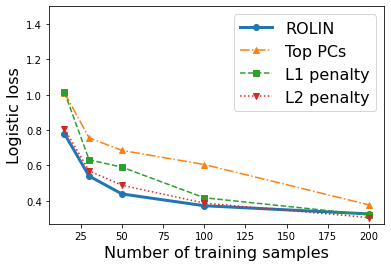
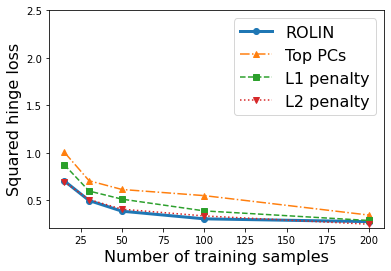
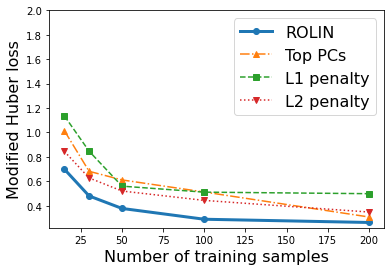
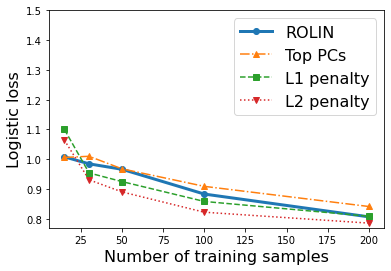
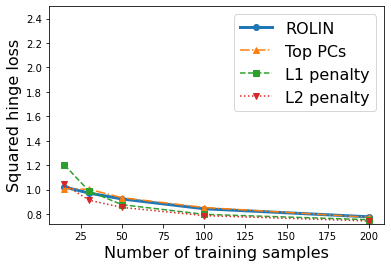
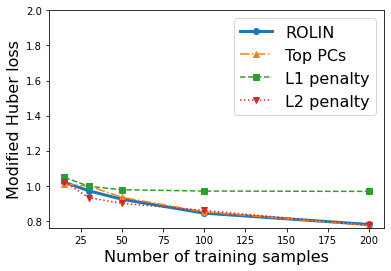
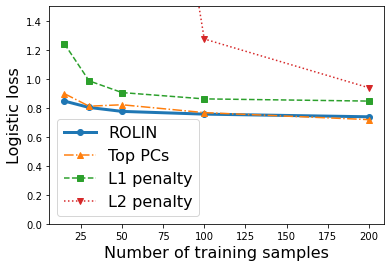
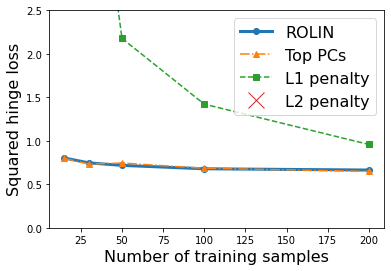
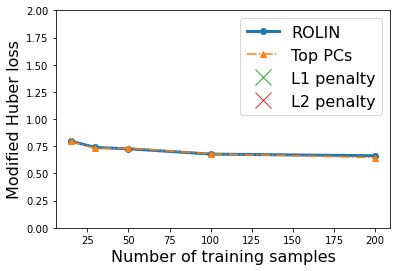
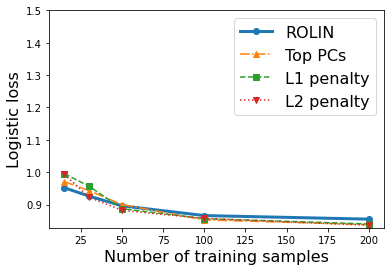
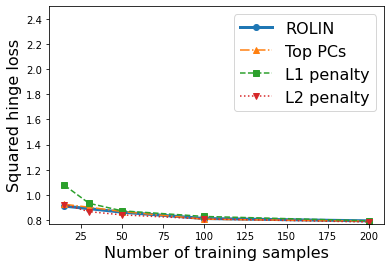
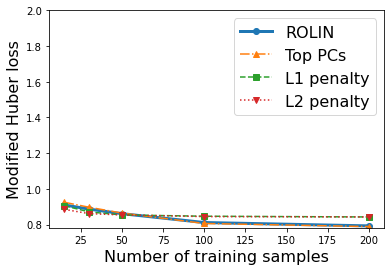
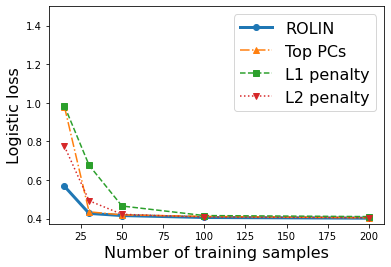
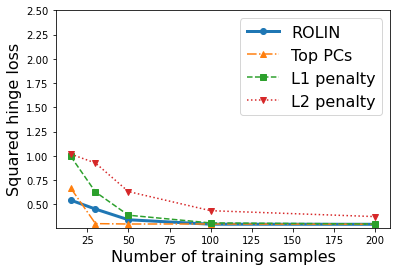
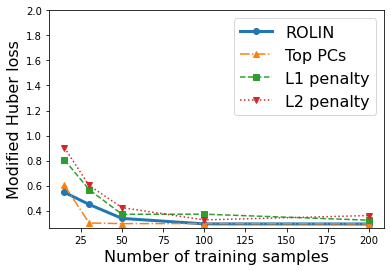
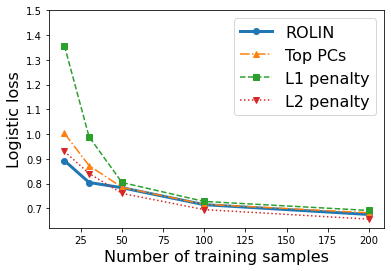
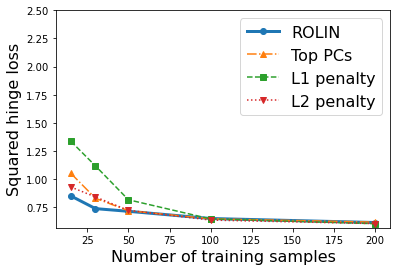
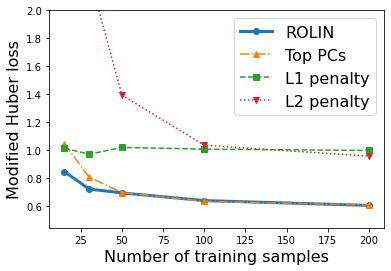
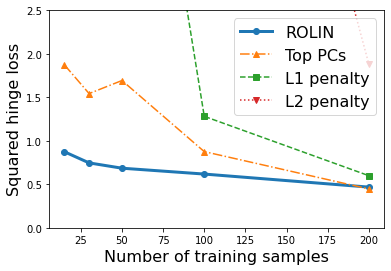
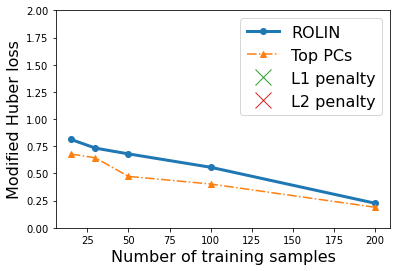
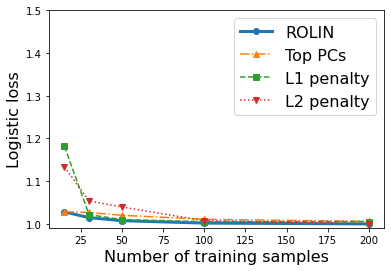
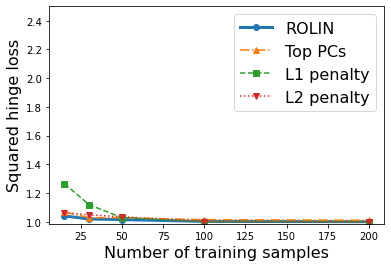
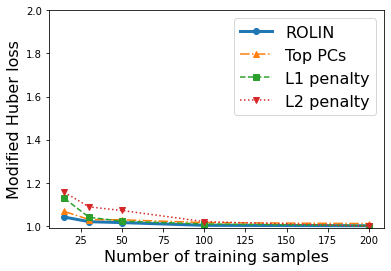
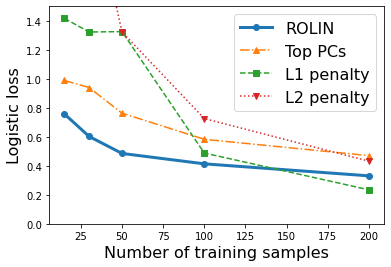
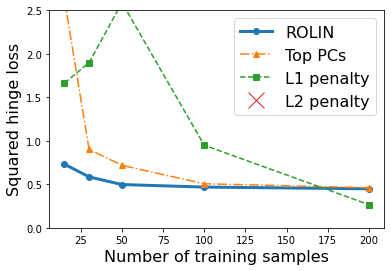
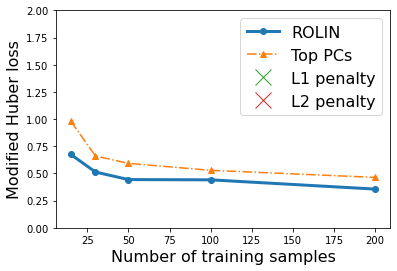
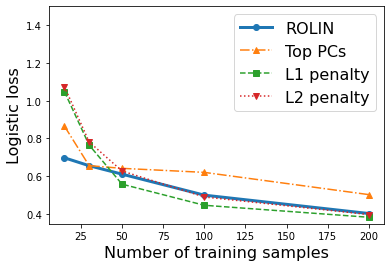
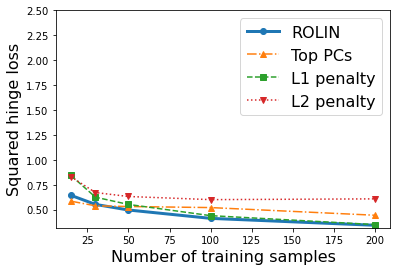
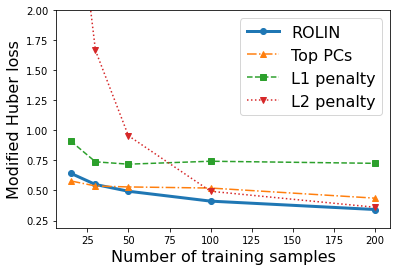
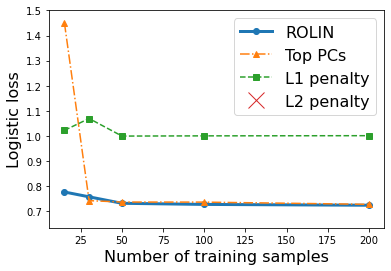
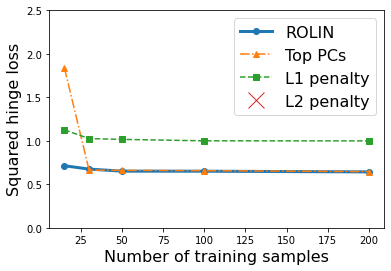
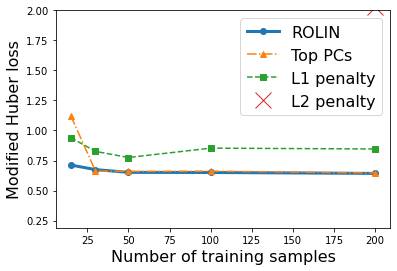
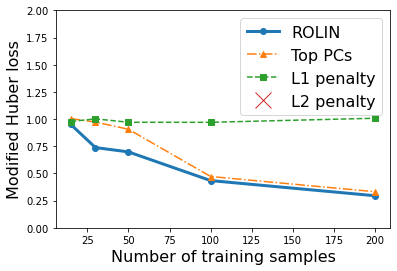
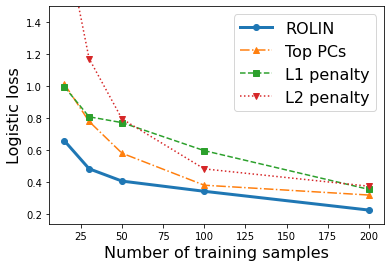
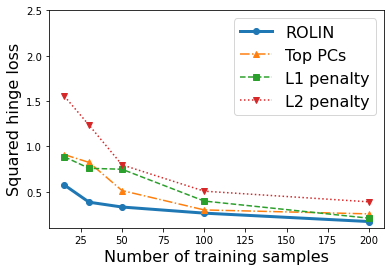
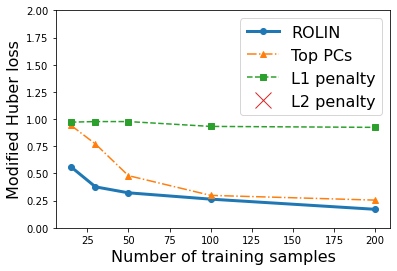
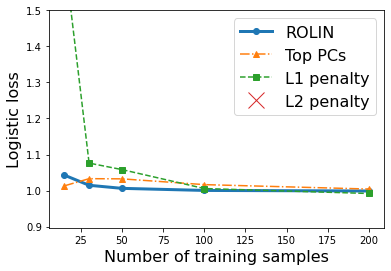
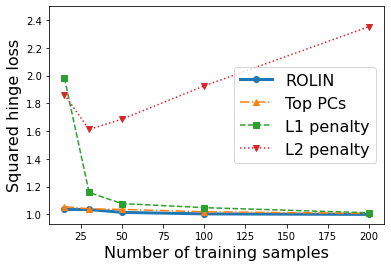
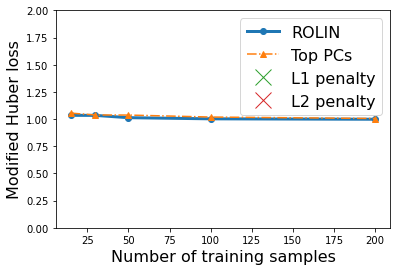
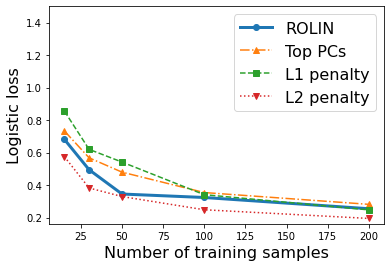
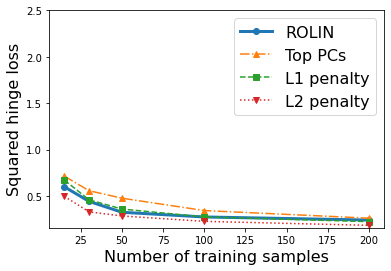
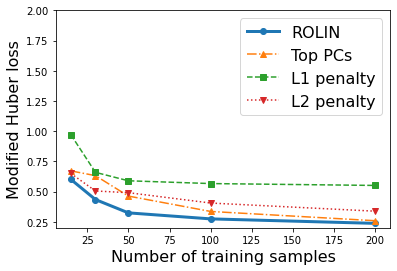
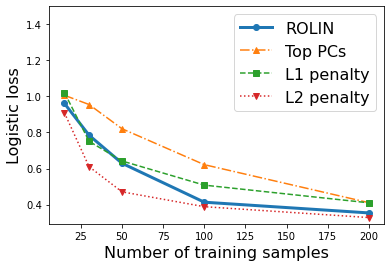
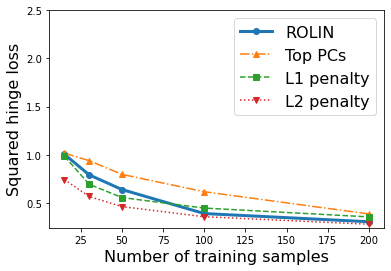
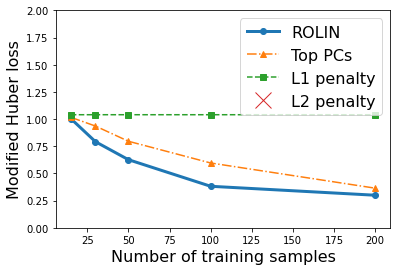
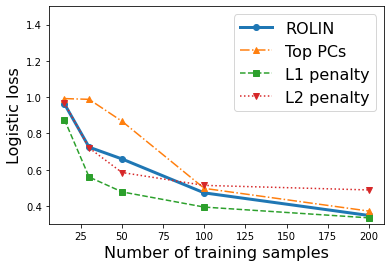
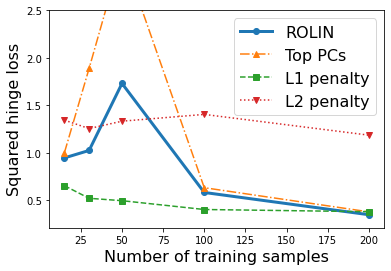
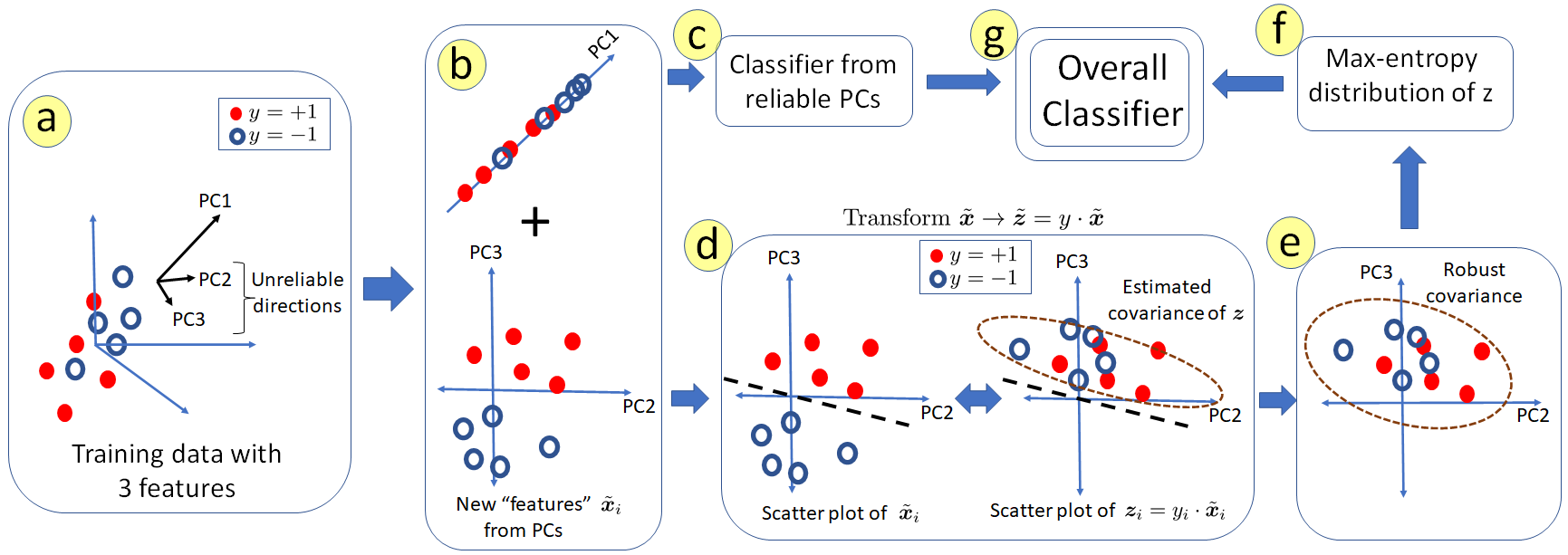
We consider the problem of linear classification under general loss functions in the limited-data setting. Overfitting is a common problem here. The standard approaches to prevent overfitting are dimensionality reduction and regularization. But dimensionality reduction loses information, while regularization requires the user to choose a norm, or a prior, or a distance metric. We propose an algorithm called RoLin that needs no user choice and applies to a large class of loss functions. RoLin combines reliable information from the top principal components with a robust optimization to extract any useful information from unreliable subspaces. It also includes a new robust cross-validation that is better than existing cross-validation methods in the limited-data setting. Experiments on $25$ real-world datasets and three standard loss functions show that RoLin broadly outperforms both dimensionality reduction and regularization. Dimensionality reduction has $14\%-40\%$ worse test loss on average as compared to RoLin. Against $L_1$ and $L_2$ regularization, RoLin can be up to 3x better for logistic loss and 12x better for squared hinge loss. The differences are greatest for small sample sizes, where RoLin achieves the best loss on 2x to 3x more datasets than any competing method. For some datasets, RoLin with $15$ training samples is better than the best norm-based regularization with $1500$ samples.
翻译:我们考虑在有限数据设置中的一般损失函数下的线性分类问题。 过度配置是一个常见的问题。 防止过度配置的标准方法是维度减少和正规化。 但是, 维度减少会丢失信息, 而规范化则要求用户选择规范, 或先行, 或距离度度度。 我们提议了一个名为RoLin 的算法, 它不需要用户选择, 并且适用于大量的损失函数。 RoLin 将来自顶层主构件的可靠信息与强力优化结合起来, 以便从不可靠的子空间中提取任何有用的信息。 它还包括一种新的稳健的交叉校验方法, 比在有限数据设置中现有的交叉校验方法要好得多。 关于25美元真实世界数据集和三个标准损失函数的实验表明, RoLin 大体上超越了维度减少和正规化两者的功能。 与罗林 相比, 平均度减少的测试损失比 $1美元 和$2美元 。 RoL 常规化比 15 的样本要好, RoL 的差别比最小的样本比 3 的样本要大。