Trade-off between prediction and FDR for high-dimensional Gaussian model selection

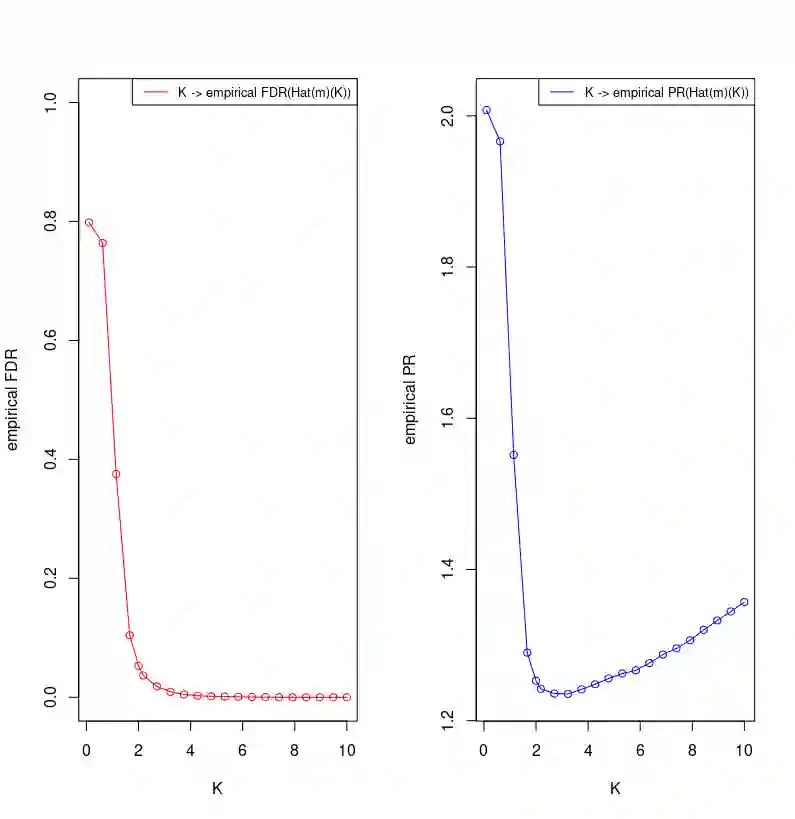
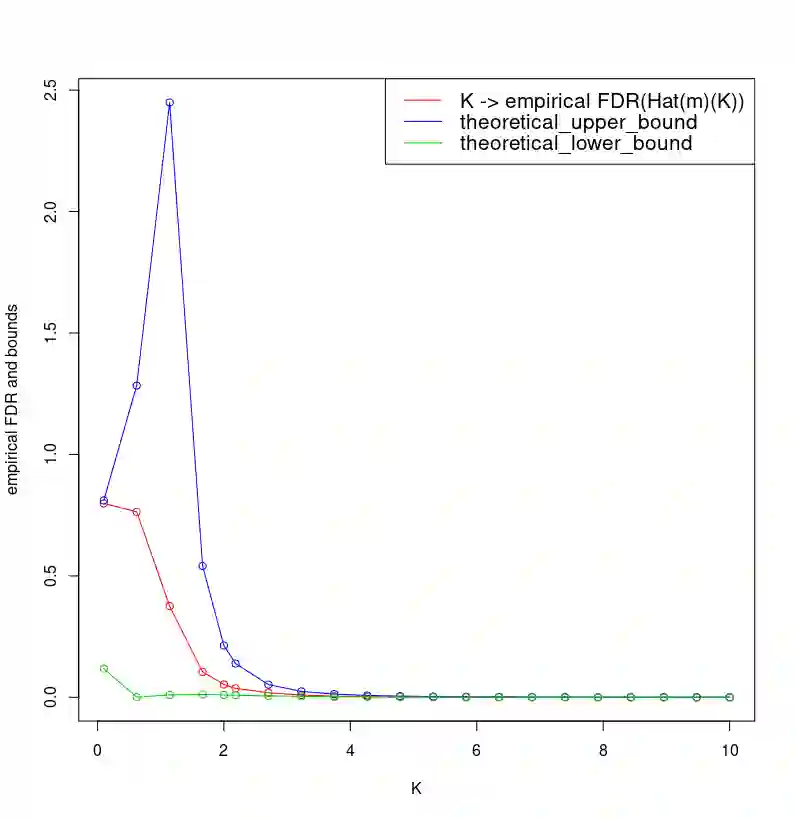
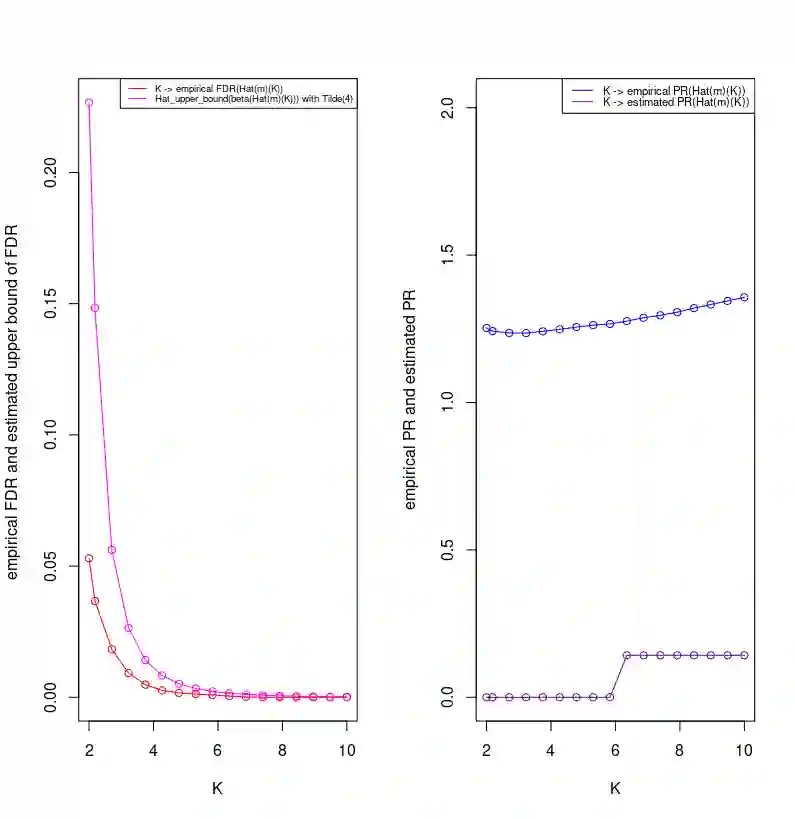
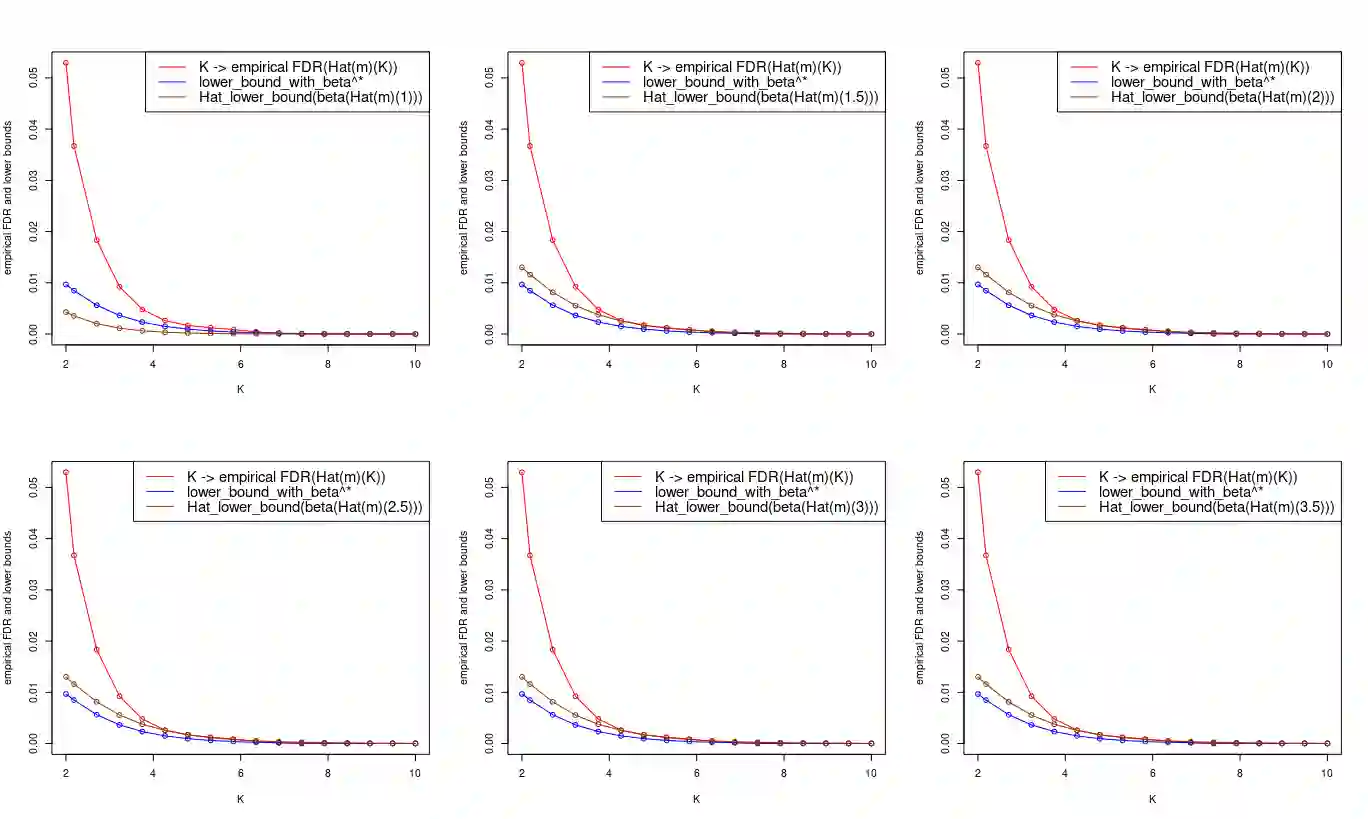
In the context of the high-dimensional Gaussian linear regression for ordered variables, we study the variable selection procedure via the minimization of the penalized least-squares criterion. We focus on model selection where we propose to control predictive risk and False Discovery Rate simultaneously. For this purpose, we obtain a convenient trade-off thanks to a proper calibration of the hyperparameter K appearing in the penalty function. We obtain non-asymptotic theoretical bounds on the False Discovery Rate with respect to K. We then provide an algorithm for the calibration of K. It is based on completely observable quantities in view of applications. Our algorithm is validated by an extensive simulation study.