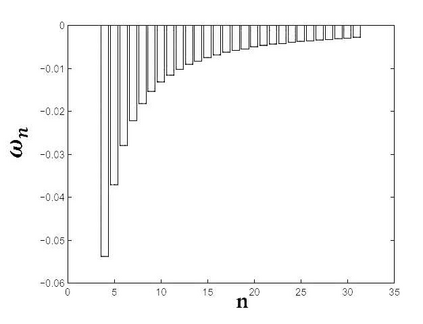
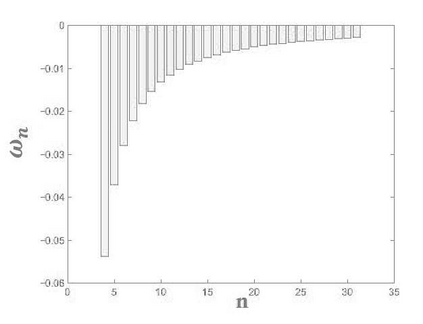
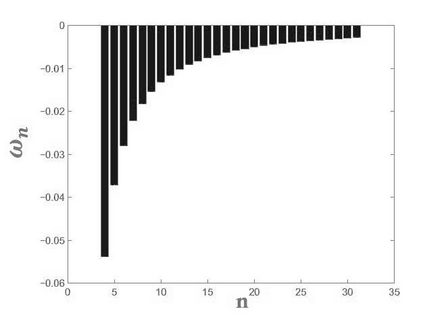
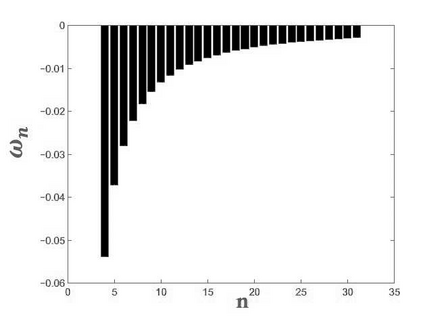
In this paper, we propose numerical scheme for the Riesz space fractional advection-dispersion equations with delay (RFADED). Firstly, analytical solution for RFADED in terms of the functions of Mittag-Leffler type is derived. Secondly, the fractional backward differential formulas (FBDF) method and shifted Gr\"{u}nwald method are introduced to the Riesz space fractional derivatives. Next, stability and convergency of these methods have been proved. Thirdly, Crank-Nicolson scheme for solving this problem is proposed. We prove that the scheme is conditionally stable and convergent with the order accuracy of ${\rm O}({\kappa ^2} + {h^2})$. Finally, some numerical results are given to demonstrate that presented method is a computationally efficient and accurate method for solving RFADED.
翻译:在本文中,我们提议了Riesz空间分解分解分布方程式的数值方案(RFADED)。首先,从Mittag-Leffler 类型函数的角度为Risz空间分解分布方程式(RFADED)提供了分析解决方案。其次,将分向后偏差公式(FBDF)方法和转移的Gr\"{u}nwald方法引入了Riesz空间分解衍生物。其次,这些方法的稳定性和趋同性得到了证明。第三,提出了解决这一问题的Crank-Nicolson方案。我们证明,这个方案有条件地稳定,并且与$\rm O}(~kapa+{h%2}+{h%2}的顺序精度一致。最后,提供了一些数字结果,以证明所提出的方法是一种计算高效和准确的解决RFADDEDD的方法。