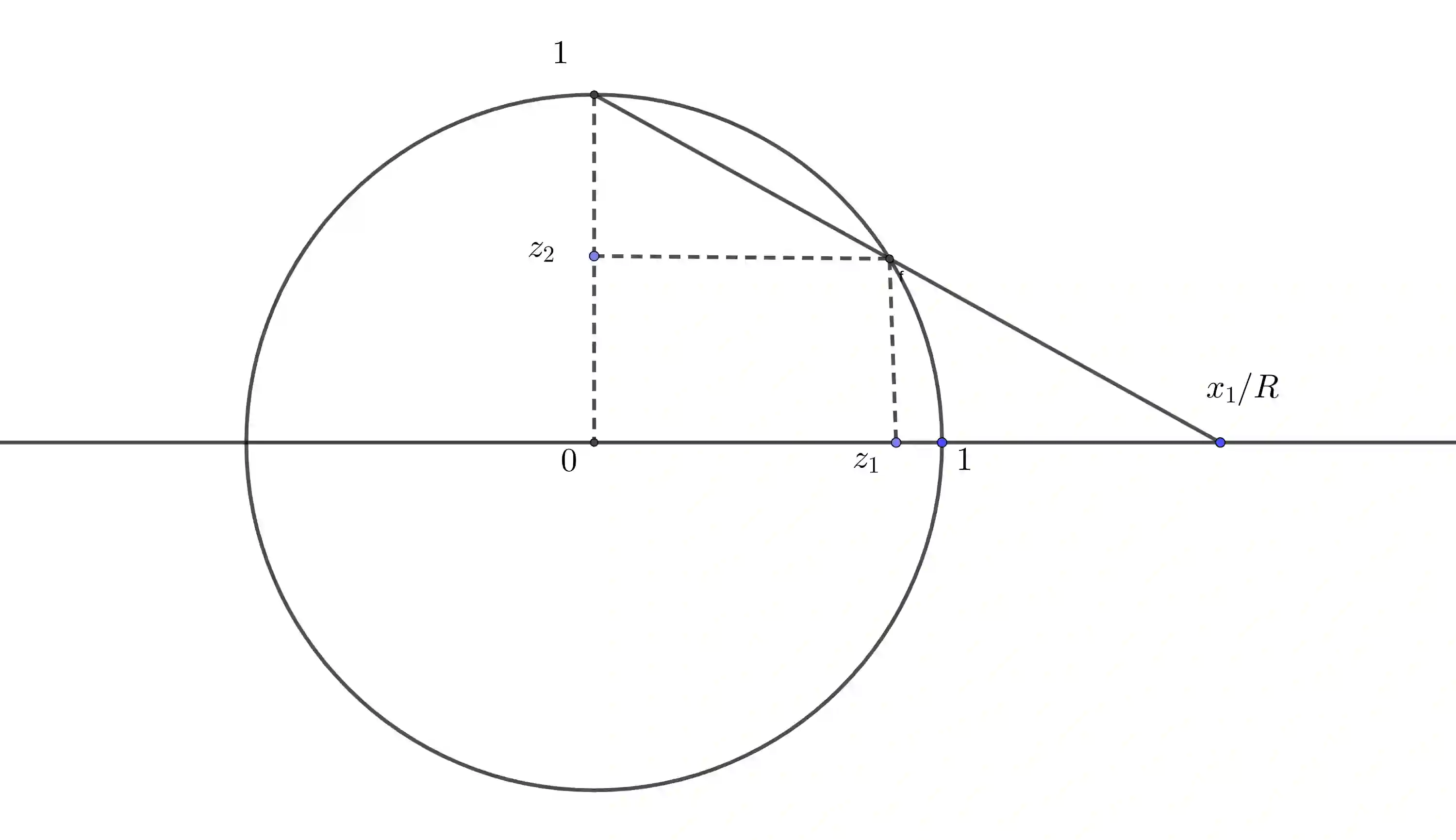
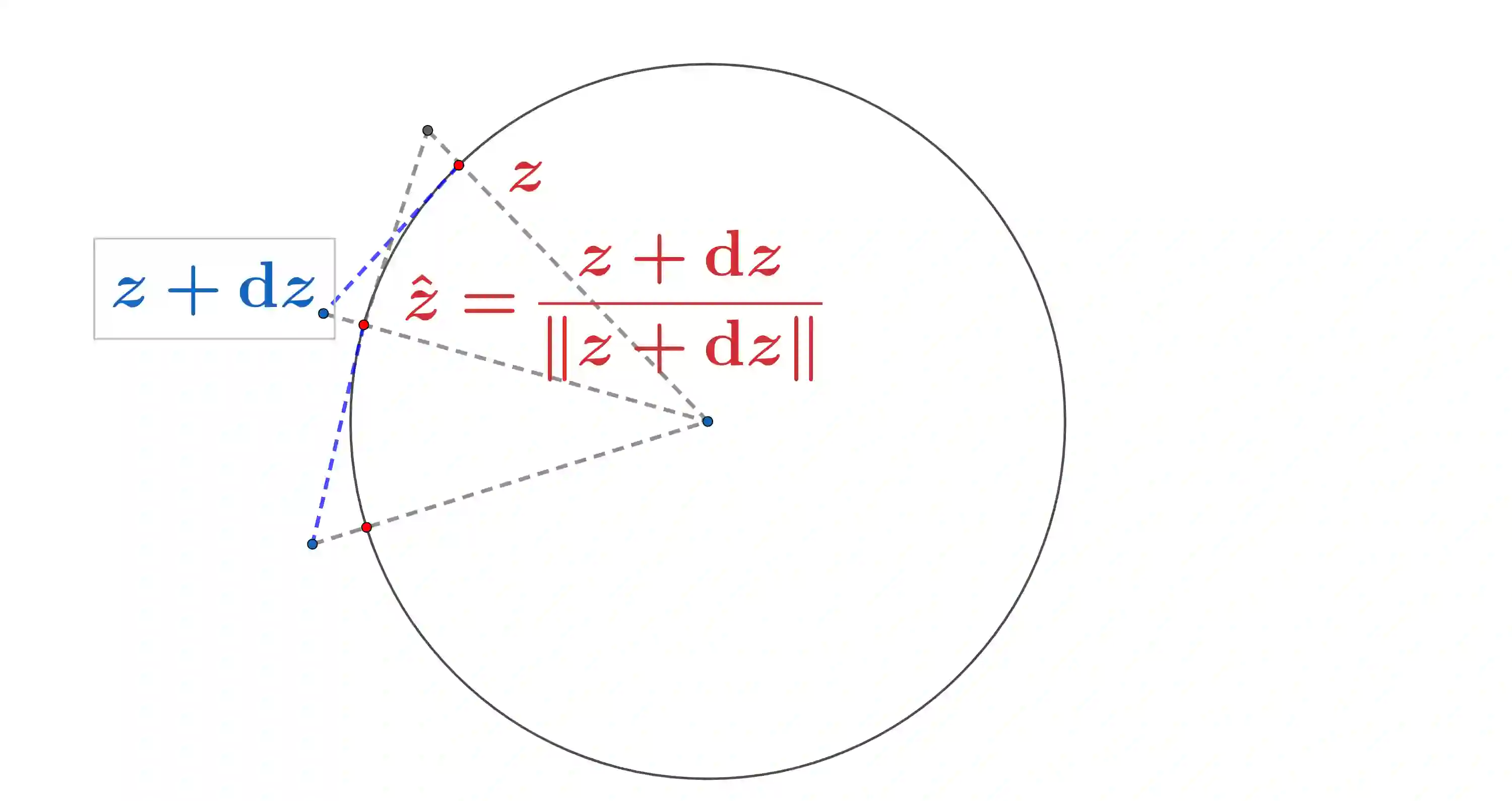
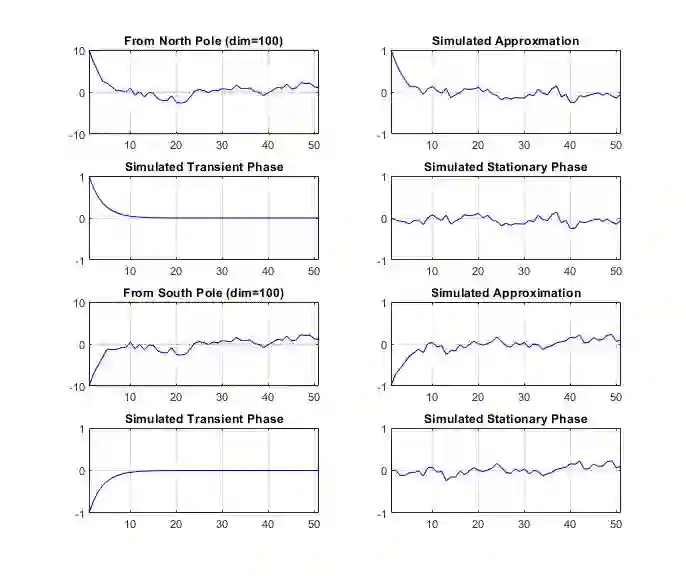
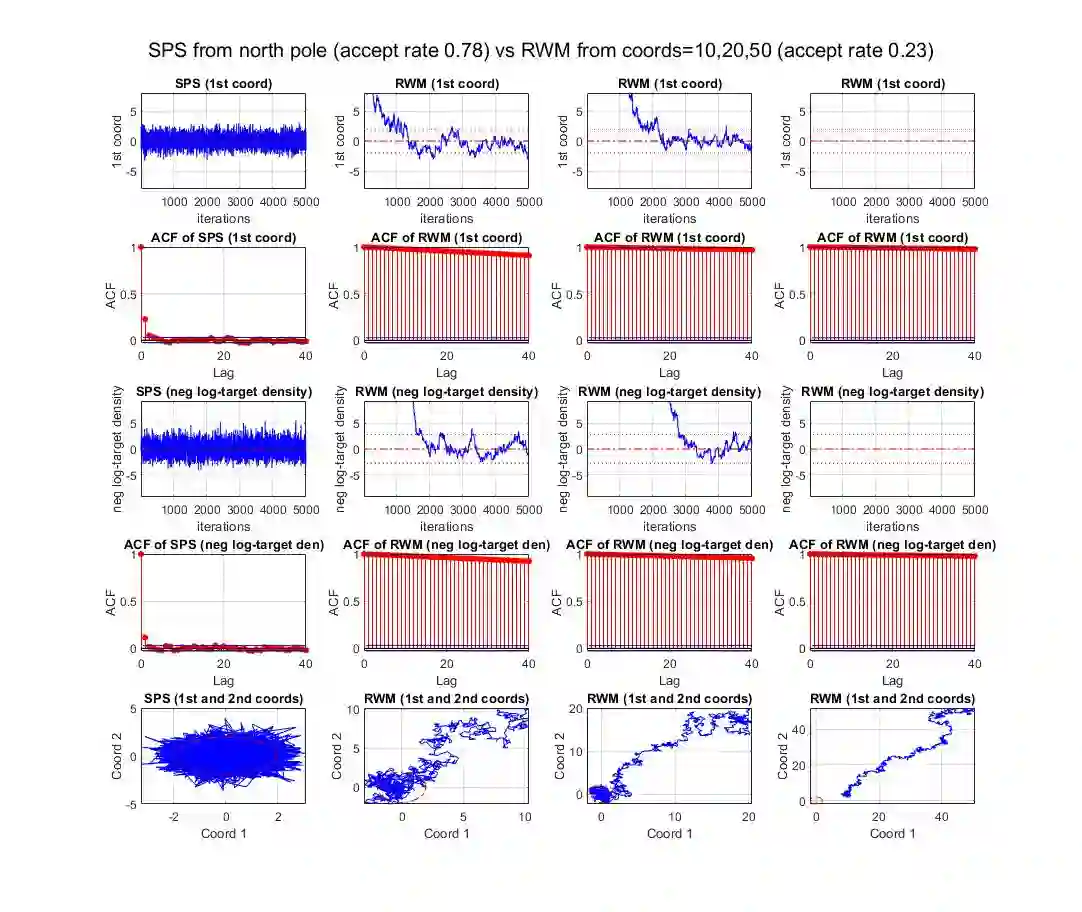
High dimensional distributions, especially those with heavy tails, are notoriously difficult for off-the-shelf MCMC samplers: the combination of unbounded state spaces, diminishing gradient information, and local moves, results in empirically observed "stickiness" and poor theoretical mixing properties -- lack of geometric ergodicity. In this paper, we introduce a new class of MCMC samplers that map the original high dimensional problem in Euclidean space onto a sphere and remedy these notorious mixing problems. In particular, we develop random-walk Metropolis type algorithms as well as versions of Bouncy Particle Sampler that are uniformly ergodic for a large class of light and heavy-tailed distributions and also empirically exhibit rapid convergence in high dimensions. In the best scenario, the proposed samplers can enjoy the ``blessings of dimensionality'' that the mixing time decreases with dimension.
翻译:高维分布,特别是那些有重尾巴的高度分布,对于现成的MCMC采样者来说,是十分困难的。 高维分布,特别是对于现成的MCMC采样者来说:将未封闭的状态空间、递减梯度信息和地方移动结合起来,导致经验观测到的“粘性”和理论混合特性差,缺乏几何性能。在本文中,我们引入了一个新的MC采样器类别,将Euclidean原高维度问题映射到一个球体上,并纠正这些臭名昭著的混合问题。特别是,我们开发了随机行的Meopolis类型算法以及各种博尼粒子采样器,这些方法对于大型的轻量和重量的分布具有统一性,而且根据经验也显示出高度的快速趋同性。在最佳情况下,拟议的采样者可以享受“光度”的维度,即混合时间随着维度减少。