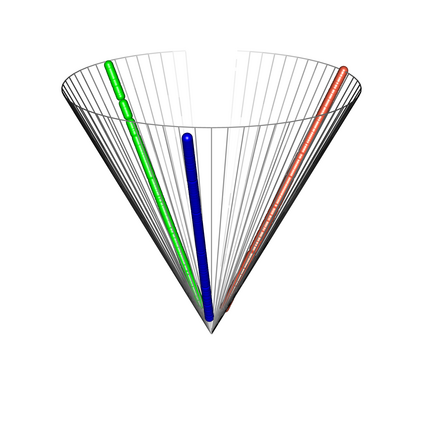
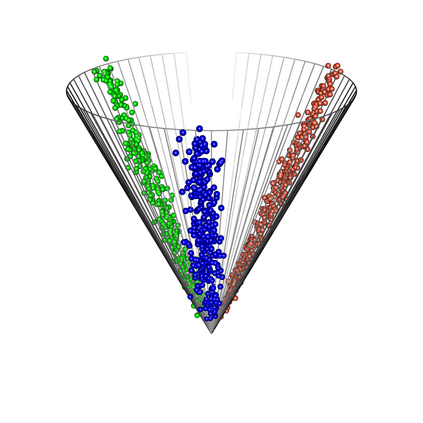
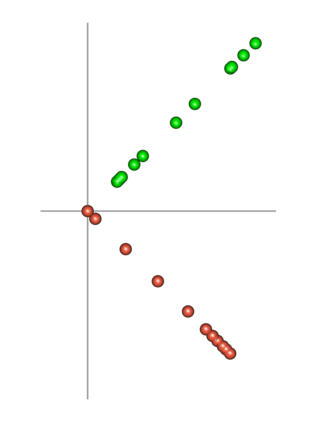
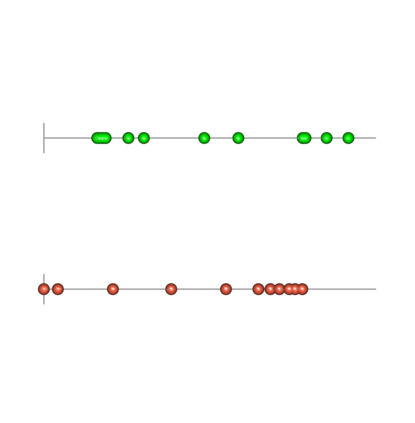
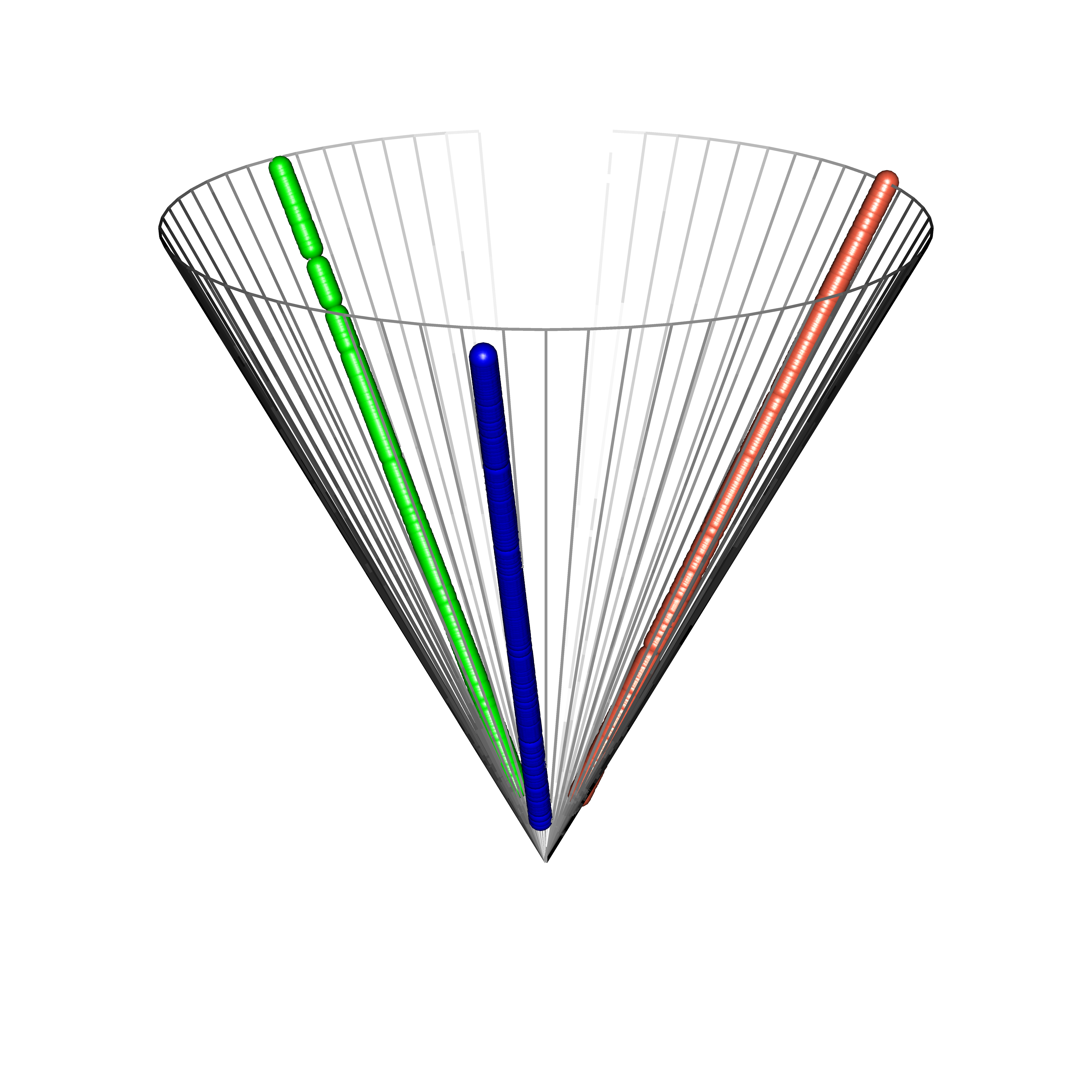
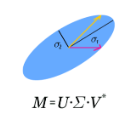
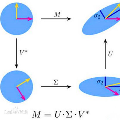
Spectral embedding finds vector representations of the nodes of a network, based on the eigenvectors of its adjacency or Laplacian matrix, and has found applications throughout the sciences. Many such networks are multipartite, meaning their nodes can be divided into partitions and nodes of the same partition are never connected. When the network is multipartite, this paper demonstrates that the node representations obtained via spectral embedding live near partition-specific low-dimensional subspaces of a higher-dimensional ambient space. For this reason we propose a follow-on step after spectral embedding, to recover node representations in their intrinsic rather than ambient dimension, proving uniform consistency under a low-rank, inhomogeneous random graph model. Our method naturally generalizes bipartite spectral embedding, in which node representations are obtained by singular value decomposition of the biadjacency or bi-Laplacian matrix.
翻译:光谱嵌入发现一个网络的节点的矢量表示, 以其相邻或拉平板矩阵的分流器为基础, 并在整个科学中找到了应用。 许多这样的网络是多部分的, 意思是它们的节点可以分割成分割区, 而同一分区的节点从没有连接。 当网络是多部分时, 本文显示通过光谱嵌入获得的节点表示 生活在一个高维环境空间的分区特定低维次空间附近。 为此, 我们提议在光谱嵌入后采取后续步骤, 以恢复其内在而非环境维度的节点表示, 证明在低层次、 混合的随机图样模型下的一致性。 我们的方法自然地将双部分光谱嵌入, 其节点表示通过对相邻或双层矩阵的奇值分解定位获得。