Gray--Wyner and Mutual Information Regions for Doubly Symmetric Binary Sources and Gaussian Sources

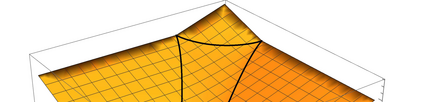
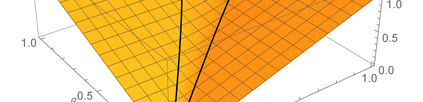
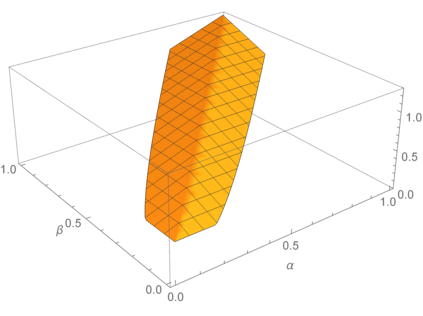
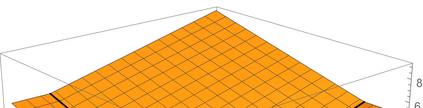
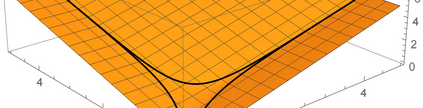
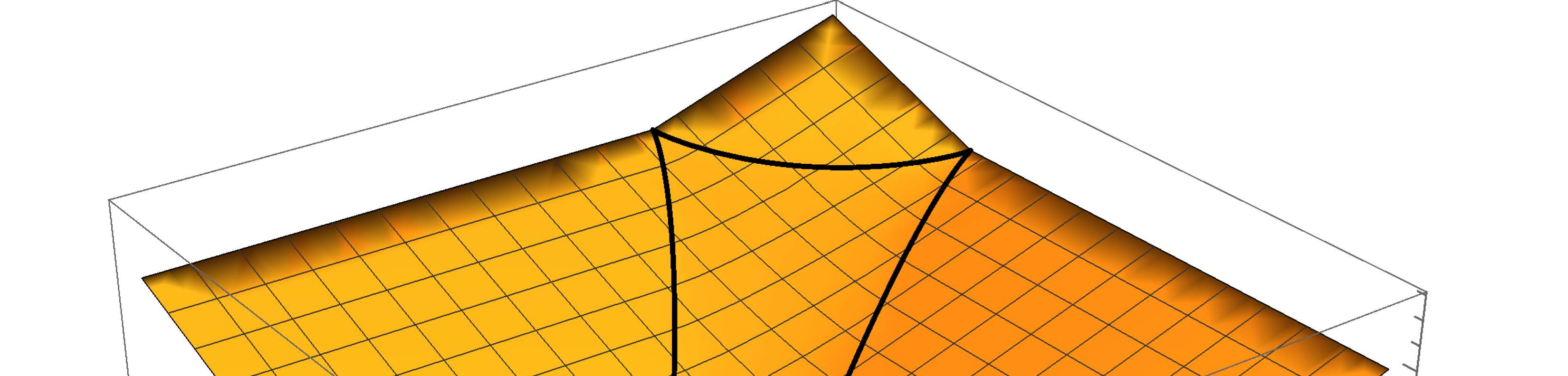
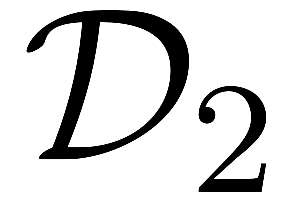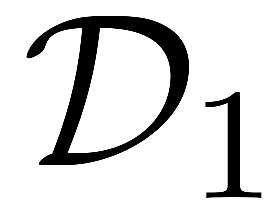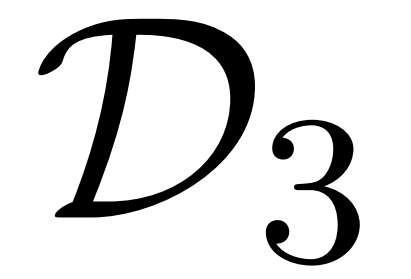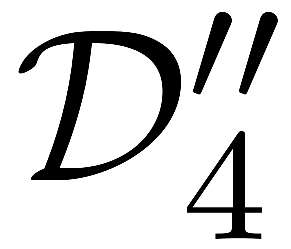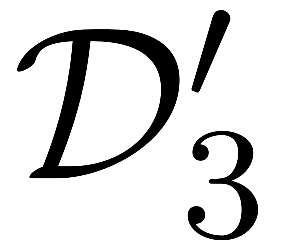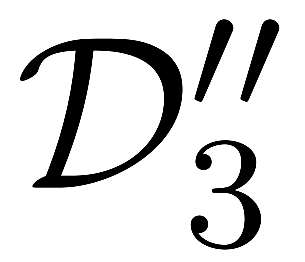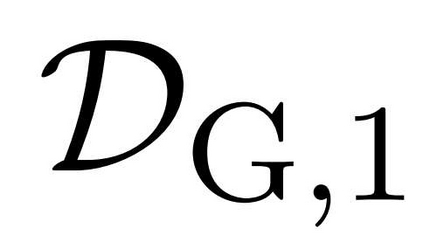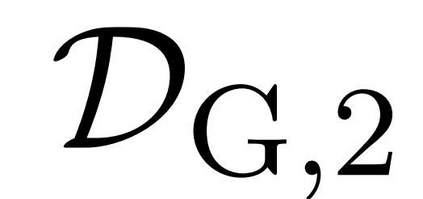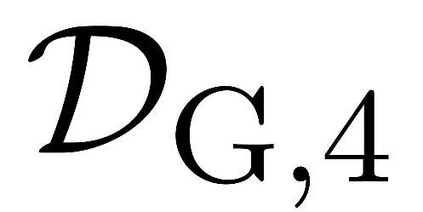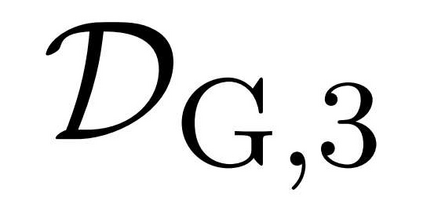Nonconvex optimization plays a key role in multi-user information theory and related fields, but it is usually difficult to solve. The rate region of the Gray--Wyner source coding system is a typical example in nonconvex optimization, whose single-letter expression was given by Gray and Wyner. However, due to the nonconvexity of the optimization involved in this expression, previously, there was none nontrivial source for which the analytic expression is known. In this paper, we prove the analytic expression for the doubly symmetric binary source (DSBS), which confirms positively a conjecture of Gray and Wyner in 1974. We also provide (or recover) the analytic expressions for more general regions, the mutual information region and the lossy Gray--Wyner region, for both the DSBS and Gaussian source. Our proof relies an auxiliary measure technique, which is coupled with the analytical expression of the optimal-transport divergence region to show the desired results.