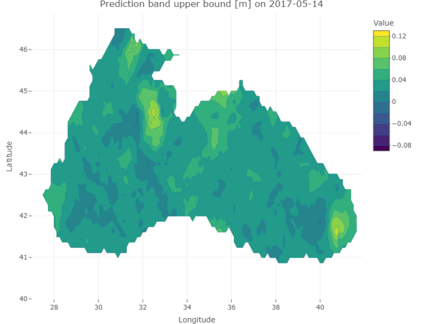
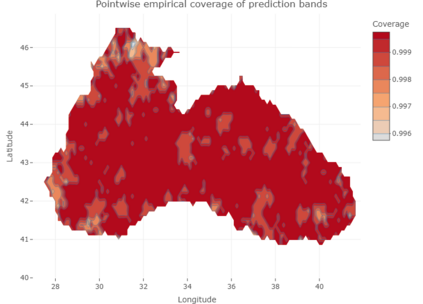
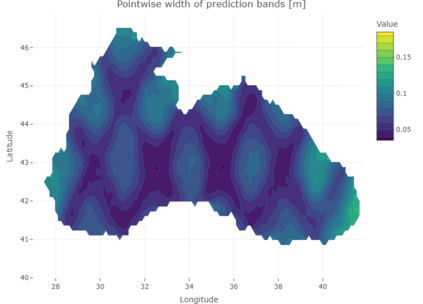
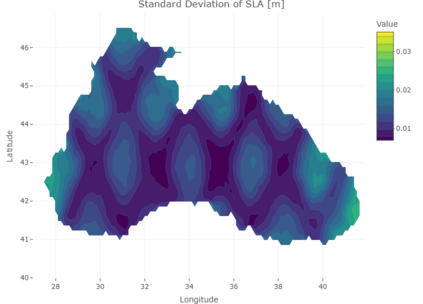
Conformal Prediction (CP) is a versatile nonparametric framework used to quantify uncertainty in prediction problems. In this work, we provide an extension of such method to the case of time series of functions defined on a bivariate domain, by proposing for the first time a distribution-free technique which can be applied to time-evolving surfaces. In order to obtain meaningful and efficient prediction regions, CP must be coupled with an accurate forecasting algorithm, for this reason, we extend the theory of autoregressive processes in Hilbert space in order to allow for functions with a bivariate domain. Given the novelty of the subject, we present estimation techniques for the Functional Autoregressive model (FAR). A simulation study is implemented, in order to investigate how different point predictors affect the resulting prediction bands. Finally, we explore benefits and limits of the proposed approach on a real dataset, collecting daily observations of Sea Level Anomalies of the Black Sea in the last twenty years.
翻译:共变预测(CP)是用于量化预测问题的不确定性的多功能、非参数框架。在这项工作中,我们首次提出可以适用于时间变化表层的无分布式技术,将这种方法扩大到双轨域界定的功能的时间序列。为了获得有意义和高效的预测区域,CP必须与准确的预测算法相结合,因此,我们扩展了希尔伯特空间的自动回归过程理论,以允许使用双轨域的功能。鉴于这个主题的新颖性,我们提出了功能自动递减模型的估算技术。进行了模拟研究,以调查不同点预测器如何影响由此产生的预测波段。最后,我们探索了拟议方法在真实数据集上的益处和局限性,收集了过去二十年来对黑海海平面异常现象的日常观测。