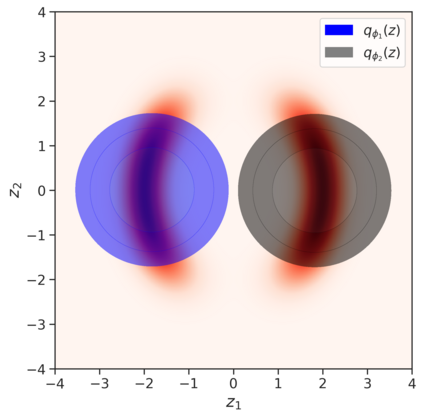
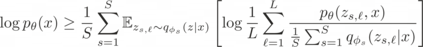In variational inference (VI), the marginal log-likelihood is estimated using the standard evidence lower bound (ELBO), or improved versions as the importance weighted ELBO (IWELBO). We propose the multiple importance sampling ELBO (MISELBO), a \textit{versatile} yet \textit{simple} framework. MISELBO is applicable in both amortized and classical VI, and it uses ensembles, e.g., deep ensembles, of independently inferred variational approximations. As far as we are aware, the concept of deep ensembles in amortized VI has not previously been established. We prove that MISELBO provides a tighter bound than the average of standard ELBOs, and demonstrate empirically that it gives tighter bounds than the average of IWELBOs. MISELBO is evaluated in density-estimation experiments that include MNIST and several real-data phylogenetic tree inference problems. First, on the MNIST dataset, MISELBO boosts the density-estimation performances of a state-of-the-art model, nouveau VAE. Second, in the phylogenetic tree inference setting, our framework enhances a state-of-the-art VI algorithm that uses normalizing flows. On top of the technical benefits of MISELBO, it allows to unveil connections between VI and recent advances in the importance sampling literature, paving the way for further methodological advances. We provide our code at \url{https://github.com/Lagergren-Lab/MISELBO}.
翻译:在变异推断框架(VI)中,边际日志可能性是使用标准证据较低约束值(ELBO)或改进版本来估计的,因为其重要性是加权的ELBO(IWELBO) 。我们建议使用多重重要性取样 ELBO(MIELBO),这是一个标准ELBO(MISELBO) 的平均值, 但它提供比IWELBO的平均值更紧密的界限。 MISELBO(MISELBO) 适用于摊销和经典VI, 它使用密度估计实验, 包括MNIST和若干独立推断的直观模型, 或经独立推断的变异性直观直观。 据我们所知, 重心的六号中深度组合概念尚未确立。 我们证明MISELBO(MILBO) 提供了比标准ELBO(ELBO) 的平均值更紧密的界限。 MISELBO(VI) 的深度测算框架中, 我们的深度测算(O(VI) II) 的深度测算(O) 的深度数据模型, 提供了我们的精度框架(VI) 的精度(O) 的精度(UILILILILA) 的精度的精度的精度的精度的精度的精度的精度。