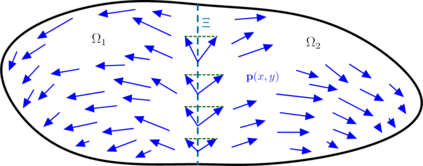
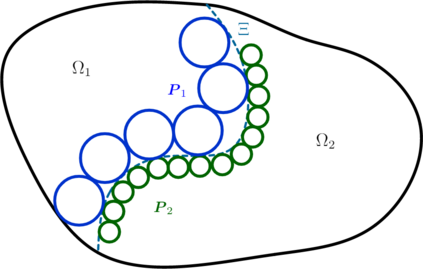
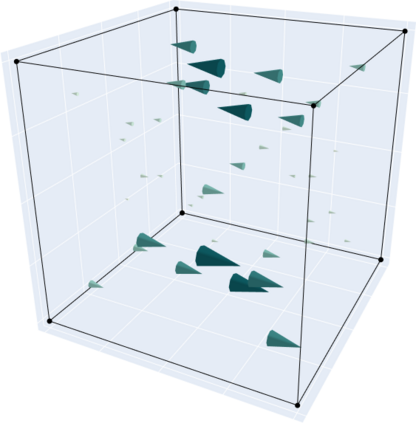
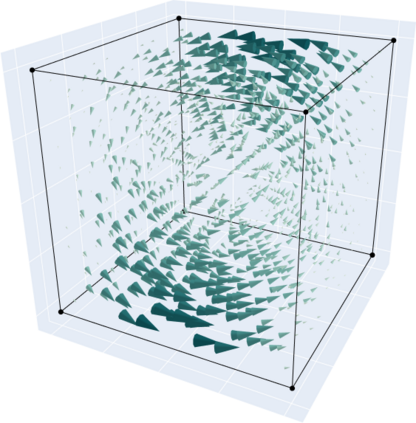
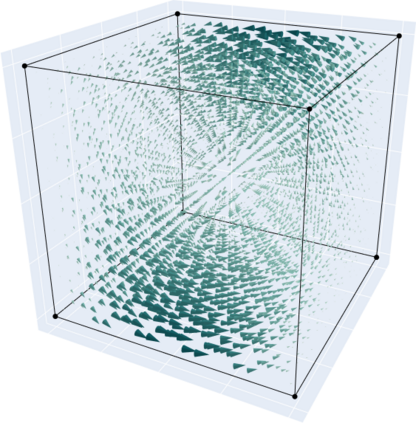
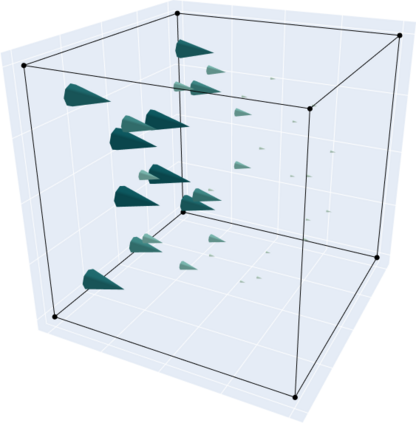
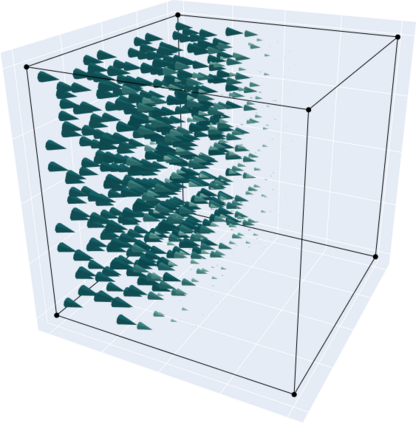
In this work we test the numerical behaviour of matrix-valued fields approximated by finite element subspaces of $[\mathit{H}^1]^{3\times 3}$, $[\mathit{H}(\mathrm{curl})]^3$ and $\mathit{H}(\mathrm{sym}\mathrm{Curl})$ for a linear abstract variational problem connected to the relaxed micromorphic model. The formulation of the corresponding finite elements is introduced, followed by numerical benchmarks and our conclusions. The relaxed micromorphic continuum model reduces the continuity assumptions of the classical micromorphic model by replacing the full gradient of the microdistortion in the free energy functional with the Curl. This results in a larger solution space for the microdistortion, namely $[\mathit{H}(\mathrm{curl})]^3$ in place of the classical $[\mathit{H}^1]^{3\times 3}$. The continuity conditions on the microdistortion can be further weakened by taking only the symmetric part of the Curl. As shown in recent works, the new appropriate space for the microdistortion is then $\mathit{H}(\mathrm{sym}\mathrm{Curl})$. The newly introduced space gives rise to a new differential complex for the relaxed micromorphic continuum theory.
翻译:在这项工作中,我们测试了以 $[$\ mathit{H ⁇ 1}}} ⁇ 3} 3} 美元、 $[[\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
相关内容
Source: Apple - iOS 8