Meta-Reinforcement Learning with Self-Modifying Networks

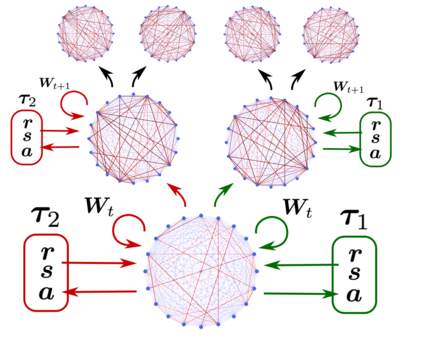
Deep Reinforcement Learning has demonstrated the potential of neural networks tuned with gradient descent for solving complex tasks in well-delimited environments. However, these neural systems are slow learners producing specialised agents with no mechanism to continue learning beyond their training curriculum. On the contrary, biological synaptic plasticity is persistent and manifold, and has been hypothesised to play a key role in executive functions such as working memory and cognitive flexibility, potentially supporting more efficient and generic learning abilities. Inspired by this, we propose to build networks with dynamic weights, able to continually perform self-reflexive modification as a function of their current synaptic state and action-reward feedback, rather than a fixed network configuration. The resulting model, MetODS (for Meta-Optimized Dynamical Synapses) is a broadly applicable meta-reinforcement learning system able to learn efficient and powerful control rules in the agent policy space. A single layer with dynamic synapses can perform one-shot learning, generalize navigation principles to unseen environments and demonstrate a strong ability to learn adaptive motor policies, comparing favourably with previous meta-reinforcement learning approaches.