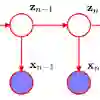
Systems of interacting continuous-time Markov chains are a powerful model class, but inference is typically intractable in high dimensional settings. Auxiliary information, such as noisy observations, is typically only available at discrete times, and incorporating it via a Doob's $h-$transform gives rise to an intractable posterior process that requires approximation. We introduce Latent Interacting Particle Systems, a model class parameterizing the generator of each Markov chain in the system. Our inference method involves estimating look-ahead functions (twist potentials) that anticipate future information, for which we introduce an efficient parameterization. We incorporate this approximation in a twisted Sequential Monte Carlo sampling scheme. We demonstrate the effectiveness of our approach on a challenging posterior inference task for a latent SIRS model on a graph, and on a neural model for wildfire spread dynamics trained on real data.
翻译:交互连续时间马尔可夫链系统是一类强大的模型,但在高维场景下其推断通常难以处理。辅助信息(如含噪声的观测)通常仅在离散时间点可用,通过Doob的$h-$变换将其纳入后,会产生一个难以处理、需要近似的后验过程。我们提出了潜在交互粒子系统,该类模型对系统中每个马尔可夫链的生成元进行参数化。我们的推断方法涉及估计能够预判未来信息的向前看函数(扭曲势),为此我们引入了一种高效的参数化方案。我们将此近似纳入一个扭曲的序贯蒙特卡罗采样框架中。我们在一个图结构上潜在SIRS模型具有挑战性的后验推断任务上,以及一个基于真实数据训练的林火蔓延动力学神经模型上,验证了我们方法的有效性。