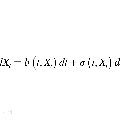Schr\"odinger Bridge (SB) is an entropy-regularized optimal transport problem that has received increasing attention in deep generative modeling for its mathematical flexibility compared to the Scored-based Generative Model (SGM). However, it remains unclear whether the optimization principle of SB relates to the modern training of deep generative models, which often rely on constructing log-likelihood objectives.This raises questions on the suitability of SB models as a principled alternative for generative applications. In this work, we present a novel computational framework for likelihood training of SB models grounded on Forward-Backward Stochastic Differential Equations Theory - a mathematical methodology appeared in stochastic optimal control that transforms the optimality condition of SB into a set of SDEs. Crucially, these SDEs can be used to construct the likelihood objectives for SB that, surprisingly, generalizes the ones for SGM as special cases. This leads to a new optimization principle that inherits the same SB optimality yet without losing applications of modern generative training techniques, and we show that the resulting training algorithm achieves comparable results on generating realistic images on MNIST, CelebA, and CIFAR10. Our code is available at https://github.com/ghliu/SB-FBSDE.
翻译:Schrödinger桥(SB)是一种熵正则化的最优输运问题,在深度生成建模中因其数学灵活性而受到越来越多的关注,相比得分为基础的生成模型(SGM)。然而,目前仍不清楚SB的优化原则是否与现代深度生成模型的训练相关,这些模型通常依赖于构建对数似然目标。这引发了SB模型作为生成应用的原则性替代方案的适用性问题。在这项工作中,我们提出了一种基于前向-后向随机微分方程理论的新型计算框架,用于实现SB模型的似然训练 - 这是一种在随机最优控制中出现的数学方法,它将SB的最优性条件转化为一组随机微分方程。关键是,这些随机微分方程可以用来构建SB的似然目标,而出人意料的是,这些目标可以概括SGM的目标作为特殊情况。这导致了一种新的优化原则,它继承了同样的SB最优性,但没有失去现代生成训练技术的应用,我们展示了所得到的训练算法在MNIST,CelebA和CIFAR10等生成逼真图像方面获得了可比的结果。我们的代码可在https://github.com/ghliu/SB-FBSDE上找到。