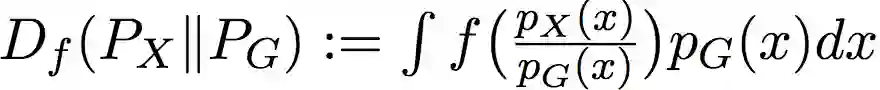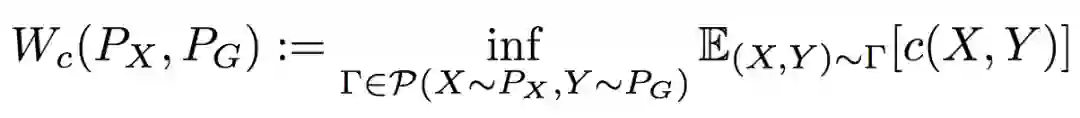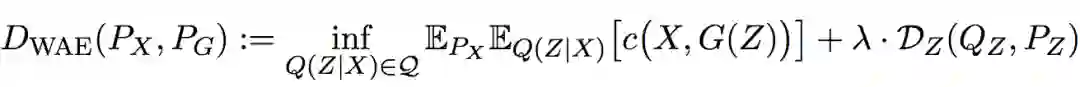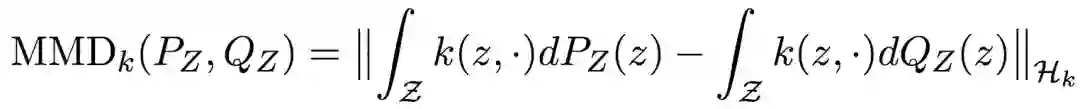马普与Google Brain新研究：Wasserstein自动编码器

来源：arXiv

编译：weakish

表征学习领域的进展，最初由监督学习推动，基于大量标注过的数据集取得了令人印象深刻的结果。另一方面，无监督学习长期以来一直基于概率方法处理低维数据。近几年来，这两种方法呈现出一种融合的趋势。变分自动编码器（variational auto-encoders），简称VAE，属于无监督学习方法，却能处理大量的图像数据，而且理论上也很优雅。不过，VAE也有缺点，应用于自然图像时，VAE生成的图像通常比较模糊。生成对抗网络（generative adversarial network，GANs）倒是能生成质量更高的图像，但不带编码器，训练起来也更困难，也饱受“模态崩塌”（模型无法刻画真实数据分布的所有多样性）之苦。

有鉴于此，马克斯普朗克学会与Google Brain的研究人员（Ilya Tolstikhin、Olivier Bousquet、Sylvain Gelly、Bernhard Schoelkopf）新提出了Wasserstein Auto-Encoder模型，能够生成画质更佳的图像样本。本文为ICLR 2018十佳论文，作者也将在ICLR 2018上作口头报告。

模型架构

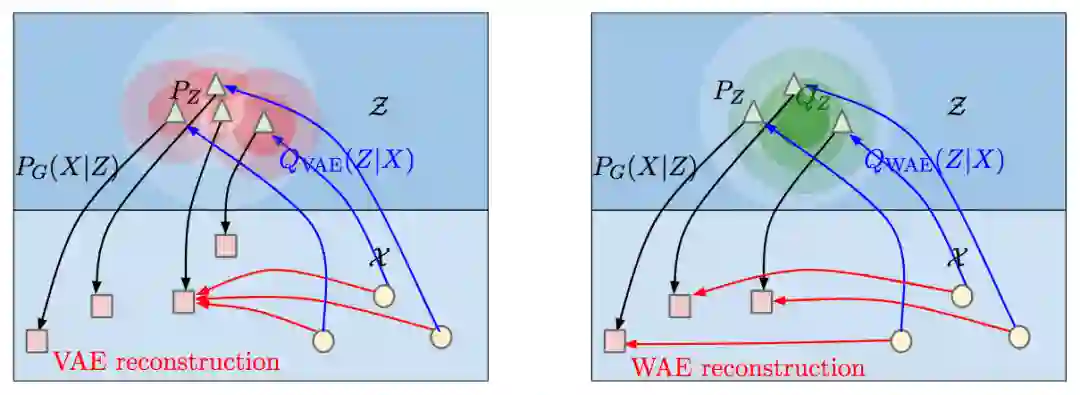
通过与VAE比较，可能更容易理解WAE的模型架构。VAE和WAE的目标均为最小化两项：

1. 重建损失函数

2. 先验分布P_Z与编码器Q引入的分布的差异（更准确地说，是一个惩罚差异的正则子）

对所有从P_X中取样的不同的输入样本x，VAE都迫使Q(Z | X = x)匹配P_Z。（上图左侧的红色圆形表示Q_Z，白色三角形表示P_Z。）相反，WAE迫使连续的混合分布Q_Z匹配P_Z（如上图右侧的绿色圆形所示），因而不同样本的潜编码可能彼此相距较远，得以更好地进行重建。

了解WAE的基本架构后，我们可以详细讨论WAE最小化的两个目标：重建损失和正则子。

首先是重建损失。为了衡量重建损失，我们需要衡量两个概率分布（原输入数据的概率分布P_X和重建数据的概率分布P_G）之间的距离。

衡量距离最常用的两类方法是f-散度（f-divergences）和optimal transport（OT）。

f散度的定义为：

其中，f是满足f(1) = 0的凸函数。f-散度常见的例子有KL散度（Kullback-Leibler divergence）和JS散度（Jenson-Shannon divergence）。

OT的定义为：

其中，c(x, y)为损失函数。当p ≥ 1时，若c(x, y) = d^p(x, y)，则称为Wasserstein距离。

研究人员精心设计了模型，简化了OT运算，最终的基于Wasserstein距离的计算目标为：

类似VAE，编码器Q和解码器G的参数由深度神经网络估计。

然后我们讨论正则子。研究人员提出了两种正则子D_Z(Q_Z, P_Z)。

1. 基于GAN的D_Z。令D_Z(Q_Z, P_Z) = D_JS(Q_Z, P_Z)，（D_JK为JK散度），然后使用对抗训练加以逼近。

2. 基于MMD的D_Z。令D_Z(P_Z, Q_Z) = MMD_k(P_Z, Q_Z)。其中，MMD_k(P_Z, Q_Z)通过以下公式计算：

MMD在符合正态分布的高维数据上表现出色，也比基于GAN逼近要节省算力。

具体算法如下：

def mmd_penalty(self, sample_qz, sample_pz):
    opts = self.opts
    sigma2_p = opts['pz_scale'] ** 2
    kernel = opts['mmd_kernel']
    n = utils.get_batch_size(sample_qz)
    n = tf.cast(n, tf.int32)
    nf = tf.cast(n, tf.float32)
    half_size = (n * n - n) / 2
    norms_pz = tf.reduce_sum(tf.square(sample_pz), axis=1, keep_dims=True)
    dotprods_pz = tf.matmul(sample_pz, sample_pz, transpose_b=True)
    distances_pz = norms_pz + tf.transpose(norms_pz) - 2. * dotprods_pz
    norms_qz = tf.reduce_sum(tf.square(sample_qz), axis=1, keep_dims=True)
    dotprods_qz = tf.matmul(sample_qz, sample_qz, transpose_b=True)
    distances_qz = norms_qz + tf.transpose(norms_qz) - 2. * dotprods_qz
    dotprods = tf.matmul(sample_qz, sample_pz, transpose_b=True)
    distances = norms_qz + tf.transpose(norms_pz) - 2. * dotprods
    if kernel == 'RBF':
        # Median heuristic for the sigma^2 of Gaussian kernel
        sigma2_k = tf.nn.top_k(
            tf.reshape(distances, [-1]), half_size).values[half_size - 1]
        sigma2_k += tf.nn.top_k(
            tf.reshape(distances_qz, [-1]), half_size).values[half_size - 1]
        # Maximal heuristic for the sigma^2 of Gaussian kernel
        # sigma2_k = tf.nn.top_k(tf.reshape(distances_qz, [-1]), 1).values[0]
        # sigma2_k += tf.nn.top_k(tf.reshape(distances, [-1]), 1).values[0]
        # sigma2_k = opts['latent_space_dim'] * sigma2_p
        if opts['verbose']:
            sigma2_k = tf.Print(sigma2_k, [sigma2_k], 'Kernel width:')
        res1 = tf.exp( - distances_qz / 2. / sigma2_k)
        res1 += tf.exp( - distances_pz / 2. / sigma2_k)
        res1 = tf.multiply(res1, 1. - tf.eye(n))
        res1 = tf.reduce_sum(res1) / (nf * nf - nf)
        res2 = tf.exp( - distances / 2. / sigma2_k)
        res2 = tf.reduce_sum(res2) * 2. / (nf * nf)
        stat = res1 - res2
    elif kernel == 'IMQ':
        # k(x, y) = C / (C + ||x - y||^2)
        # C = tf.nn.top_k(tf.reshape(distances, [-1]), half_size).values[half_size - 1]
        # C += tf.nn.top_k(tf.reshape(distances_qz, [-1]), half_size).values[half_size - 1]
        Cbase = 2 * opts['zdim'] * sigma2_p
        stat = 0.
        for scale in [.1, .2, .5, 1., 2., 5., 10.]:
            C = Cbase * scale
            res1 = C / (C + distances_qz)
            res1 += C / (C + distances_pz)
            res1 = tf.multiply(res1, 1. - tf.eye(n))
            res1 = tf.reduce_sum(res1) / (nf * nf - nf)
            res2 = C / (C + distances)
            res2 = tf.reduce_sum(res2) * 2. / (nf * nf)
            stat += res1 - res2
    return stat
def gan_penalty(self, sample_qz, sample_pz):
    opts = self.opts
    # Pz = Qz test based on GAN in the Z space
    logits_Pz = z_adversary(opts, sample_pz)
    logits_Qz = z_adversary(opts, sample_qz, reuse=True)
    loss_Pz = tf.reduce_mean(
        tf.nn.sigmoid_cross_entropy_with_logits(
            logits=logits_Pz, labels=tf.ones_like(logits_Pz)))
    loss_Qz = tf.reduce_mean(
        tf.nn.sigmoid_cross_entropy_with_logits(
            logits=logits_Qz, labels=tf.zeros_like(logits_Qz)))
    loss_Qz_trick = tf.reduce_mean(
        tf.nn.sigmoid_cross_entropy_with_logits(
            logits=logits_Qz, labels=tf.ones_like(logits_Qz)))
    loss_adversary = self.wae_lambda * (loss_Pz + loss_Qz)
    # Non-saturating loss trick
    loss_match = loss_Qz_trick
    return (loss_adversary, logits_Pz, logits_Qz), loss_match

试验结果

研究人员在MNIST和CelebA数据集上试验了WAE：

可以看到，WAE重建的图像画质高于VAE。

研究人员也采用FID（Frechet Inception Distance）评分对模型CelebA上的表现进行了定量评估：（FID值越小意味着表现越好）

算法	FID
VAE	82
WAE-MMD	55
WAE-GAN	42

论文、代码

论文发表在预印本文库 arXiv:1711.01558

作者开源了WAE实现（基于TensorFlow）: github.com/tolstikhin/wae